湖北省天门、仙桃、潜江、江汉油田2020年中考数学试卷
试卷更新日期:2020-08-04 类型:中考真卷
一、选择题
-
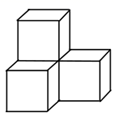
1. 下列各数中,比-2小的数是( )A、0 B、-3 C、-1 D、2. 如图是由4个相同的小正方体组成的立体图形,它的俯视图为( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为( )A、 B、 C、 D、4. 将一副三角尺如图摆放,点E在 上,点D在 的延长线上, ,则 的度数是( )
3. 我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒.数3000000用科学记数法表示为( )A、 B、 C、 D、4. 将一副三角尺如图摆放,点E在 上,点D在 的延长线上, ,则 的度数是( )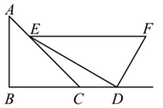 A、15° B、20° C、25° D、30°5. 下列说法正确的是( )A、为了解人造卫星的设备零件的质量情况,选择抽样调查 B、方差是刻画数据波动程度的量 C、购买一张体育彩票必中奖,是不可能事件 D、掷一枚质地均匀的硬币,正面朝上的概率为16. 下列运算正确的是( )A、 B、 C、 D、7. 对于一次函数 ,下列说法不正确的是( )A、图象经过点 B、图象与x轴交于点 C、图象不经过第四象限 D、当 时,8. 一个圆锥的底面半径是 ,其侧面展开图的圆心角是120°,则圆锥的母线长是( )A、 B、 C、 D、9. 关于x的方程 有两个实数根 , ,且 ,那么m的值为( )A、-1 B、-4 C、-4或1 D、-1或410. 如图,已知 和 都是等腰三角形, , 交于点F,连接 ,下列结论:① ;② ;③ 平分 ;④ .其中正确结论的个数有( )
A、15° B、20° C、25° D、30°5. 下列说法正确的是( )A、为了解人造卫星的设备零件的质量情况,选择抽样调查 B、方差是刻画数据波动程度的量 C、购买一张体育彩票必中奖,是不可能事件 D、掷一枚质地均匀的硬币,正面朝上的概率为16. 下列运算正确的是( )A、 B、 C、 D、7. 对于一次函数 ,下列说法不正确的是( )A、图象经过点 B、图象与x轴交于点 C、图象不经过第四象限 D、当 时,8. 一个圆锥的底面半径是 ,其侧面展开图的圆心角是120°,则圆锥的母线长是( )A、 B、 C、 D、9. 关于x的方程 有两个实数根 , ,且 ,那么m的值为( )A、-1 B、-4 C、-4或1 D、-1或410. 如图,已知 和 都是等腰三角形, , 交于点F,连接 ,下列结论:① ;② ;③ 平分 ;④ .其中正确结论的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 正n边形的一个内角等于135°,则边数n的值为 .12. 篮球联赛中,每玚比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队14场比赛得到23分,则该队胜了场.13. 如图,海中有个小岛A,一艘轮船由西向东航行,在点B处测得小岛A位于它的东北方向,此时轮船与小岛相距20海里,继续航行至点D处,测得小岛A在它的北偏西60°方向,此时轮船与小岛的距离 为海里.
 14. 有3张看上去无差别的卡片,上面分别写着2,3,4.随机抽取1张后,放回并混在一起,再随机抽取1张,则两次取出的数字之和是奇数的概率为.15. 某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为元.16. 如图,已知直线 ,直线 和点 ,过点 作y轴的平行线交直线a于点 ,过点 作x轴的平行线交直线b于点 ,过点 作y轴的平行线交直线a于点 ,过点 作x轴的平行线交直线b于点 ,…,按此作法进行下去,则点 的横坐标为.
14. 有3张看上去无差别的卡片,上面分别写着2,3,4.随机抽取1张后,放回并混在一起,再随机抽取1张,则两次取出的数字之和是奇数的概率为.15. 某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为元.16. 如图,已知直线 ,直线 和点 ,过点 作y轴的平行线交直线a于点 ,过点 作x轴的平行线交直线b于点 ,过点 作y轴的平行线交直线a于点 ,过点 作x轴的平行线交直线b于点 ,…,按此作法进行下去,则点 的横坐标为.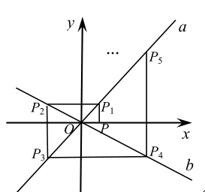
三、解答题
-
17.(1)、先化简,再求值: ,其中 .(2)、解不等式组 ,并把它的解集在数轴上表示出来.
 18. 在平行四边形 中,E为 的中点,请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.
18. 在平行四边形 中,E为 的中点,请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.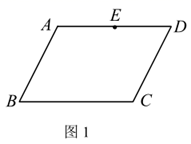
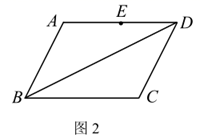 (1)、如图1,在 上找出一点M,使点M是 的中点;(2)、如图2,在 上找出一点N,使点N是 的一个三等分点.19. 5月20日九年级复学啦!为了解学生的体温情况,班主任张老师根据全班学生某天上午的《体温监测记载表》,绘制了如下不完整的频数分布表和扇形统计图.
(1)、如图1,在 上找出一点M,使点M是 的中点;(2)、如图2,在 上找出一点N,使点N是 的一个三等分点.19. 5月20日九年级复学啦!为了解学生的体温情况,班主任张老师根据全班学生某天上午的《体温监测记载表》,绘制了如下不完整的频数分布表和扇形统计图.学生体温频数分布表:
组别
温度(℃)
频数(人数)
甲
36.3
6
乙
36.4
a
丙
36.5
20
丁
36.6
4

请根据以上信息,解答下列问题:
(1)、频数分布表中 , 该班学生体温的众数是 , 中位数是;(2)、扇形统计图中 , 丁组对应的扇形的圆心角是度;(3)、求该班学生的平均体温(结果保留小数点后一位).20. 把抛物线 先向右平移4个单位长度,再向下平移5个单位长度得到抛物线 .(1)、直接写出抛物线 的函数关系式;(2)、动点 能否在拋物线 上?请说明理由;(3)、若点 都在抛物线 上,且 ,比较 的大小,并说明理由.21. 如图,在 中, ,以 为直径的⊙O交 于点D,过点D的直线 交 于点F,交 的延长线于点E,且 .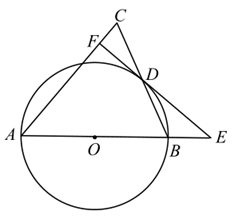 (1)、求证: 是⊙O的切线;(2)、当 时,求 的长.22. 如图,直线 与反比例函数 的图象交于A,B两点,已知点A的坐标为 , 的面积为8.
(1)、求证: 是⊙O的切线;(2)、当 时,求 的长.22. 如图,直线 与反比例函数 的图象交于A,B两点,已知点A的坐标为 , 的面积为8. (1)、填空:反比例函数的关系式为;(2)、求直线 的函数关系式;(3)、动点P在y轴上运动,当线段 与 之差最大时,求点P的坐标.23. 实践操作:第一步:如图1,将矩形纸片 沿过点D的直线折叠,使点A落在 上的点 处,得到折痕 ,然后把纸片展平.第二步:如图2,将图1中的矩形纸片 沿过点E的直线折叠,点C恰好落在 上的点 处,点B落在点 处,得到折痕 , 交 于点M, 交 于点N,再把纸片展平.
(1)、填空:反比例函数的关系式为;(2)、求直线 的函数关系式;(3)、动点P在y轴上运动,当线段 与 之差最大时,求点P的坐标.23. 实践操作:第一步:如图1,将矩形纸片 沿过点D的直线折叠,使点A落在 上的点 处,得到折痕 ,然后把纸片展平.第二步:如图2,将图1中的矩形纸片 沿过点E的直线折叠,点C恰好落在 上的点 处,点B落在点 处,得到折痕 , 交 于点M, 交 于点N,再把纸片展平.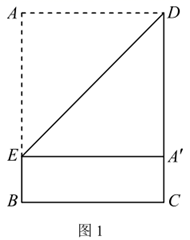

问题解决:
(1)、如图1,填空:四边形 的形状是;(2)、如图2,线段 与 是否相等?若相等,请给出证明;若不等,请说明理由;(3)、如图2,若 ,求 的值.24. 小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟.在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图1表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图2中线段 表示小华和商店的距离 (米)与时间t(分钟)的函数关系的图象的一部分,请根据所给信息解答下列问题: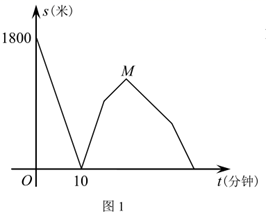
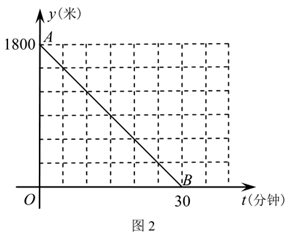 (1)、填空:妈妈骑车的速度是米/分钟,妈妈在家装载货物所用时间是分钟,点M的坐标是;(2)、直接写出妈妈和商店的距离 (米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;(3)、求t为何值时,两人相距360米.
(1)、填空:妈妈骑车的速度是米/分钟,妈妈在家装载货物所用时间是分钟,点M的坐标是;(2)、直接写出妈妈和商店的距离 (米)与时间t(分钟)的函数关系式,并在图2中画出其函数图象;(3)、求t为何值时,两人相距360米.