湖北省黄石市2020年中考数学试卷
试卷更新日期:2020-08-04 类型:中考真卷
一、选择题
-
1. 3的相反数是( ).A、 B、3 C、 D、2. 下列图形中,既是中心对称又是轴对称图形的是( )A、
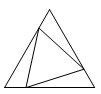 B、
B、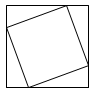 C、
C、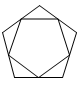 D、
D、 3. 如图所示,该几何体的俯视图是( )
3. 如图所示,该几何体的俯视图是( )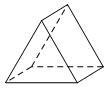 A、
A、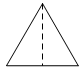 B、
B、 C、
C、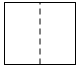 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 函数 的自变量x的取值范围是( )A、 ,且 B、 C、 D、 ,且6. 不等式组 的解集是( )A、 B、 C、 D、7. 在平面直角坐标系中,点G的坐标是 ,连接 ,将线段 绕原点O旋转 ,得到对应线段 ,则点 的坐标为( )A、 B、 C、 D、8. 如图,在 中, ,点H、E、F分别是边 、 、 的中点,若 ,则 的值为( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 函数 的自变量x的取值范围是( )A、 ,且 B、 C、 D、 ,且6. 不等式组 的解集是( )A、 B、 C、 D、7. 在平面直角坐标系中,点G的坐标是 ,连接 ,将线段 绕原点O旋转 ,得到对应线段 ,则点 的坐标为( )A、 B、 C、 D、8. 如图,在 中, ,点H、E、F分别是边 、 、 的中点,若 ,则 的值为( )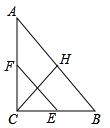 A、3 B、4 C、5 D、69. 如图,点A、B、C在 上, ,垂足分别为D、E,若 ,则 的度数为( )
A、3 B、4 C、5 D、69. 如图,点A、B、C在 上, ,垂足分别为D、E,若 ,则 的度数为( )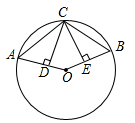 A、 B、 C、 D、10. 若二次函数 的图象,过不同的六点 、 、 、 、 、 ,则 、 、 的大小关系是( )A、 B、 C、 D、
A、 B、 C、 D、10. 若二次函数 的图象,过不同的六点 、 、 、 、 、 ,则 、 、 的大小关系是( )A、 B、 C、 D、二、填空题
-
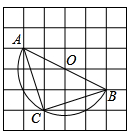
11. 计算: .12. 因式分解: .13. 据报道,2020年4月9日下午,黄石市重点园区(珠三角)云招商财富推介会上,我市现场共签项目20个,总投资137.6亿元,用科学记数法表示137.6亿元,可写为元.14. 某中学规定学生体育成绩满分为100分,按课外活动成绩、期中成绩、期末成绩 的比,计算学期成绩.小明同学本学期三项成绩依次为90分、90分、80分,则小明同学本学期的体育成绩是分.15. 如图,在 的方格纸中,每个小方格都是边长为1的正方形,其中A、B、C为格点,作 的外接圆,则 的长等于.
 16. 匈牙利著名数学家爱尔特希(P. Erdos,1913-1996)曾提出:在平面内有n个点,其中每三个点都能构成等腰三角形,人们将具有这样性质的n个点构成的点集称为爱尔特希点集.如图,是由五个点A、B、C、D、O构成的爱尔特希点集(它们为正五边形的任意四个顶点及正五边形的中心构成),则 的度数是.
16. 匈牙利著名数学家爱尔特希(P. Erdos,1913-1996)曾提出:在平面内有n个点,其中每三个点都能构成等腰三角形,人们将具有这样性质的n个点构成的点集称为爱尔特希点集.如图,是由五个点A、B、C、D、O构成的爱尔特希点集(它们为正五边形的任意四个顶点及正五边形的中心构成),则 的度数是.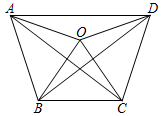
三、解答题
-
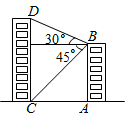
17. 先化简,再求值: ,其中 .18. 如图,是某小区的甲、乙两栋住宅楼,小丽站在甲栋楼房 的楼顶,测量对面的乙栋楼房 的高度,已知甲栋楼房 与乙栋楼房 的水平距离 米,小丽在甲栋楼房顶部B点,测得乙栋楼房顶部D点的仰角是 ,底部C点的俯角是 ,求乙栋楼房 的高度(结果保留根号).
 19. 如图, .
19. 如图, .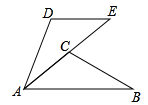 (1)、求 的度数;(2)、若 ,求证: .20. 如图,反比例函数 的图象与正比例函数 的图象相交于 、B两点,点C在第四象限,BC∥x轴.
(1)、求 的度数;(2)、若 ,求证: .20. 如图,反比例函数 的图象与正比例函数 的图象相交于 、B两点,点C在第四象限,BC∥x轴.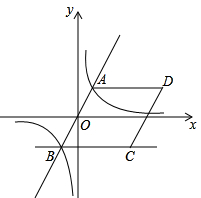 (1)、求k的值;(2)、以 、 为边作菱形 ,求D点坐标.21. 已知:关于x的一元二次方程 有两个实数根.(1)、求m的取值范围;(2)、设方程的两根为 、 ,且满足 ,求m的值.22. 我市将面向全市中小学开展“经典诵读”比赛.某中学要从2名男生2名女生共4名学生中选派2名学生参赛.(1)、请列举所有可能出现的选派结果;(2)、求选派的2名学生中,恰好为1名男生1名女生的概率.23. 我国传统数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊五,直金十六两.问牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值19两银子;2头牛、5只羊,值16两银子,问每头牛、每只羊分别值银子多少两?”
(1)、求k的值;(2)、以 、 为边作菱形 ,求D点坐标.21. 已知:关于x的一元二次方程 有两个实数根.(1)、求m的取值范围;(2)、设方程的两根为 、 ,且满足 ,求m的值.22. 我市将面向全市中小学开展“经典诵读”比赛.某中学要从2名男生2名女生共4名学生中选派2名学生参赛.(1)、请列举所有可能出现的选派结果;(2)、求选派的2名学生中,恰好为1名男生1名女生的概率.23. 我国传统数学名著《九章算术》记载:“今有牛五、羊二,直金十九两;牛二、羊五,直金十六两.问牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值19两银子;2头牛、5只羊,值16两银子,问每头牛、每只羊分别值银子多少两?”根据以上译文,提出以下两个问题:
(1)、求每头牛、每只羊各值多少两银子?(2)、若某商人准备用19两银子买牛和羊(要求既有牛也有羊,且银两须全部用完),请问商人有几种购买方法?列出所有的可能.