湖北省恩施州2020年中考数学试卷
试卷更新日期:2020-08-04 类型:中考真卷
一、选择题
-
1. 5的绝对值是( )A、 5 B、﹣5 C、 D、2. 茶中精品“恩施绿”“利川红”享誉世界.去年恩施州茶叶产量约为120000吨,将数120000用科学记数法表示为( ).A、 B、 C、 D、3. 下列交通标识,既是中心对称图形,又是轴对称图形的是( ).A、
 B、
B、 C、
C、 D、
D、 4. 下列计算正确的是( ).A、 B、 C、 D、5. 函数 的自变量的取值范围是( )A、 B、 且 C、 D、 且6. “彩缕碧筠粽,香梗白玉团”.端午佳节,小明妈妈准备了豆沙粽2个、红枣烷4个、腊肉粽3个、白米粽2个,其中豆沙粽和红枣粽是甜粽.小明任意选取一个,选到甜粽的概率是( ).A、 B、 C、 D、7. 在实数范围内定义运算“☆”: ,例如: .如果 ,则x的值是( ).A、-1 B、1 C、0 D、28. 我国古代数学著作《九章算术》“盈不足”一章中记载:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何”.意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛.问1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶盛酒x斛,1个小桶盛酒y斛,下列方程组正确的是( ).A、 B、 C、 D、9. 如图是由四个相同的小正方体组成的立体图形,它的主视图为( ).
4. 下列计算正确的是( ).A、 B、 C、 D、5. 函数 的自变量的取值范围是( )A、 B、 且 C、 D、 且6. “彩缕碧筠粽,香梗白玉团”.端午佳节,小明妈妈准备了豆沙粽2个、红枣烷4个、腊肉粽3个、白米粽2个,其中豆沙粽和红枣粽是甜粽.小明任意选取一个,选到甜粽的概率是( ).A、 B、 C、 D、7. 在实数范围内定义运算“☆”: ,例如: .如果 ,则x的值是( ).A、-1 B、1 C、0 D、28. 我国古代数学著作《九章算术》“盈不足”一章中记载:“今有大器五小器一容三斛,大器一小器五容二斛,问大小器各容几何”.意思是:有大小两种盛酒的桶,已知5个大桶加上1个小桶可以盛酒3斛,1个大桶加上5个小桶可以盛酒2斛.问1个大桶、1个小桶分别可以盛酒多少斛?设1个大桶盛酒x斛,1个小桶盛酒y斛,下列方程组正确的是( ).A、 B、 C、 D、9. 如图是由四个相同的小正方体组成的立体图形,它的主视图为( ). A、
A、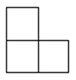 B、
B、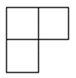 C、
C、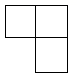 D、
D、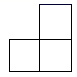 10. 甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是( ).
10. 甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是( ).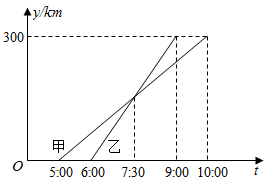 A、甲车的平均速度为 B、乙车的平均速度为 C、乙车比甲车先到 城 D、乙车比甲车先出发11. 如图,正方形 的边长为4,点E在 上且 ,F为对角线 上一动点,则 周长的最小值为( ).
A、甲车的平均速度为 B、乙车的平均速度为 C、乙车比甲车先到 城 D、乙车比甲车先出发11. 如图,正方形 的边长为4,点E在 上且 ,F为对角线 上一动点,则 周长的最小值为( ).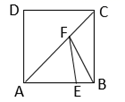 A、5 B、6 C、7 D、812. 如图,已知二次函数 的图象与x轴相交于 、 两点.则以下结论:① ;②二次函数 的图象的对称轴为 ;③ ;④ .其中正确的有( )个.
A、5 B、6 C、7 D、812. 如图,已知二次函数 的图象与x轴相交于 、 两点.则以下结论:① ;②二次函数 的图象的对称轴为 ;③ ;④ .其中正确的有( )个.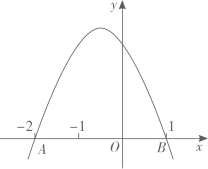 A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
13. 9的算术平方根是 , = , ﹣ = .14. 如图,直线 ,点A在直线 上,点 在直线 上, , , ,则 .
 15. 如图,已知半圆的直径 ,点C在半圆上,以点A为圆心, 为半径画弧交 于点D,连接 .若 ,则图中阴影部分的面积为.(结果不取近似值)
15. 如图,已知半圆的直径 ,点C在半圆上,以点A为圆心, 为半径画弧交 于点D,连接 .若 ,则图中阴影部分的面积为.(结果不取近似值)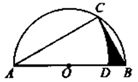 16. 如图,在平面直角坐标系中, 的顶点坐标分别为: , , .已知 ,作点N关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,…,依此类推,则点 的坐标为.
16. 如图,在平面直角坐标系中, 的顶点坐标分别为: , , .已知 ,作点N关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,点 关于点 的对称点 ,…,依此类推,则点 的坐标为.
三、解答题
-
17. 先化简,再求值: ,其中 .18. 如图, , 平分∠ABC交 于点D,点C在 上且 ,连接 .求证:四边形 是菱形.
 19. 某中学为了解九年级学生对新冠肺炎防控知识的掌握情况,从全校九年级学生中随机抽取部分学生进行调查.调查结果分为四类:A类—非常了解;B类—比较了解;C—一般了解;D类—不了解.现将调查结果绘制成如下不完整的统计图,请根据统计图中的信息解答下列问题:
19. 某中学为了解九年级学生对新冠肺炎防控知识的掌握情况,从全校九年级学生中随机抽取部分学生进行调查.调查结果分为四类:A类—非常了解;B类—比较了解;C—一般了解;D类—不了解.现将调查结果绘制成如下不完整的统计图,请根据统计图中的信息解答下列问题:
 (1)、本次共调查了名学生;(2)、补全条形统计图;(3)、D类所对应扇形的圆心角的大小为;(4)、若该校九年级学生共有500名,根据以上抽样结果,估计该校九年级学生对新冠肺炎防控知识非常了解的约有名.20. 如图,一艘轮船以每小时30海里的速度自东向西航行,在A处测得小岛 位于其西北方向(北偏西 方向),2小时后轮船到达B处,在B处测得小岛P位于其北偏东 方向.求此时船与小岛P的距离(结果保留整数,参考数据: , ).
(1)、本次共调查了名学生;(2)、补全条形统计图;(3)、D类所对应扇形的圆心角的大小为;(4)、若该校九年级学生共有500名,根据以上抽样结果,估计该校九年级学生对新冠肺炎防控知识非常了解的约有名.20. 如图,一艘轮船以每小时30海里的速度自东向西航行,在A处测得小岛 位于其西北方向(北偏西 方向),2小时后轮船到达B处,在B处测得小岛P位于其北偏东 方向.求此时船与小岛P的距离(结果保留整数,参考数据: , ).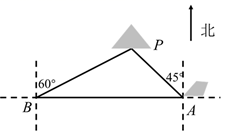 21. 如图,在平面直角坐标系中,直线 与x轴、y轴分别相交于A、B两点,与双曲线 的一个交点为C,且 .
21. 如图,在平面直角坐标系中,直线 与x轴、y轴分别相交于A、B两点,与双曲线 的一个交点为C,且 . (1)、求点A的坐标;(2)、当 时,求a和k的值.22. 某校足球队需购买A、B两种品牌的足球.已知 品牌足球的单价比B品牌足球的单价高20元,且用900元购买A品牌足球的数量用720元购买B品牌足球的数量相等.(1)、求A、B两种品牌足球的单价;(2)、若足球队计划购买A、B两种品牌的足球共90个,且A品牌足球的数量不小于B品牌足球数量的2倍,购买两种品牌足球的总费用不超过8500元.设购买A品牌足球m个,总费用为W元,则该队共有几种购买方案?采用哪一种购买方案可使总费用最低?最低费用是多少元?23. 如图, 是 的直径,直线 与 相切于点A,直线 与 相切于点B,点C(异于点A)在 上,点D在 上,且 ,延长 与 相交于点E,连接 并延长交 于点F.
(1)、求点A的坐标;(2)、当 时,求a和k的值.22. 某校足球队需购买A、B两种品牌的足球.已知 品牌足球的单价比B品牌足球的单价高20元,且用900元购买A品牌足球的数量用720元购买B品牌足球的数量相等.(1)、求A、B两种品牌足球的单价;(2)、若足球队计划购买A、B两种品牌的足球共90个,且A品牌足球的数量不小于B品牌足球数量的2倍,购买两种品牌足球的总费用不超过8500元.设购买A品牌足球m个,总费用为W元,则该队共有几种购买方案?采用哪一种购买方案可使总费用最低?最低费用是多少元?23. 如图, 是 的直径,直线 与 相切于点A,直线 与 相切于点B,点C(异于点A)在 上,点D在 上,且 ,延长 与 相交于点E,连接 并延长交 于点F.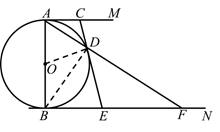 (1)、求证: 是 的切线;(2)、求证: ;(3)、如图,连接 并延长与 分别相交于点G、H,连接 .若 , ,求 .
(1)、求证: 是 的切线;(2)、求证: ;(3)、如图,连接 并延长与 分别相交于点G、H,连接 .若 , ,求 .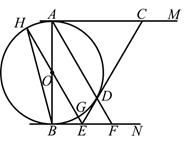 24. 如图,抛物线 经过点 ,顶点为B,对称轴 与x轴相交于点A,D为线段 的中点.
24. 如图,抛物线 经过点 ,顶点为B,对称轴 与x轴相交于点A,D为线段 的中点. (1)、求抛物线的解析式;(2)、P为线段 上任意一点,M为x轴上一动点,连接 ,以点M为中心,将 逆时针旋转 ,记点P 的对应点为E,点C的对应点为F.当直线 与抛物线 只有一个交点时,求点M的坐标.
(1)、求抛物线的解析式;(2)、P为线段 上任意一点,M为x轴上一动点,连接 ,以点M为中心,将 逆时针旋转 ,记点P 的对应点为E,点C的对应点为F.当直线 与抛物线 只有一个交点时,求点M的坐标.