贵州省毕节市2020年中考数学试卷
试卷更新日期:2020-08-04 类型:中考真卷
一、选择题
-
1. 3的倒数是( )A、 3 B、-3 C、 D、2. 中国的国土面积约为9600000平方千米,用科学记数法表示为( )A、96×105 B、0.96×107 C、9.6×106 D、9.6×1073. 下列图是由5个大小相同的小立方体搭成的几何体,主视图和左视图相同的是( )A、
 B、
B、 C、
C、 D、
D、 4. 下列图形中,是中心对称的图形的是( )
4. 下列图形中,是中心对称的图形的是( ) A、直角三角形 B、等边三角形 C、平行四边形 D、正五边形5. 已知 ,则 的值为( )A、 B、 C、 D、6. 已知 ,下列运算中正确的是( )A、 B、 C、 D、7. 将一幅直角三角板( , , ,点 在边 上)按图中所示位置摆放,两条斜边为 , ,且 ,则 等于( )
A、直角三角形 B、等边三角形 C、平行四边形 D、正五边形5. 已知 ,则 的值为( )A、 B、 C、 D、6. 已知 ,下列运算中正确的是( )A、 B、 C、 D、7. 将一幅直角三角板( , , ,点 在边 上)按图中所示位置摆放,两条斜边为 , ,且 ,则 等于( ) A、 B、 C、 D、8. 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计,制成下表:
A、 B、 C、 D、8. 某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计,制成下表:投中次数
3
5
6
7
8
9
人数
1
3
2
2
1
1
则这10名队员投中次数组成的一组数据中,众数和中位数分别为( )
A、5,6 B、2,6 C、5,5 D、6,59. 若等腰三角形中有两边长分别为3和7,则这个三角的周长为( )A、13 B、17 C、10 或 13 D、13 或 1710. 在平面直角坐标系中,第二象限内有一点M,点M到x轴的距离为5,到y轴的距离为4,则点M的坐标是( )A、 B、 C、 D、11. 如图,在矩形 中,对角线 , 相交于点O,点E,F分别是 , 的中点,连接 ,若 , ,则 的长是( ) A、 B、 C、 D、12. 某商店换季准备打折出售某商品,如果按原售价的七五折出售,将亏损25元,而按原售价的九折出售,将盈利20元,则该商品的成本为( )A、230元 B、250元 C、270元 D、300元13. 已知点C、D是以AB为直径的半圆的三等分点,弧CD的长为 ,则图中阴影部分的面积为( )
A、 B、 C、 D、12. 某商店换季准备打折出售某商品,如果按原售价的七五折出售,将亏损25元,而按原售价的九折出售,将盈利20元,则该商品的成本为( )A、230元 B、250元 C、270元 D、300元13. 已知点C、D是以AB为直径的半圆的三等分点,弧CD的长为 ,则图中阴影部分的面积为( )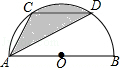 A、 B、 C、 D、14. 已知 的图象如图所示,对称轴为直线 ,若 , 是一元二次方程 的两个根,且 , ,则下列说法正确的是( )
A、 B、 C、 D、14. 已知 的图象如图所示,对称轴为直线 ,若 , 是一元二次方程 的两个根,且 , ,则下列说法正确的是( )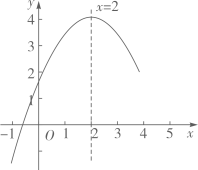 A、 B、 C、 D、15. 如图,在一个宽度为 长的小巷内,一个梯子的长为a,梯子的底端位于 上的点P,将该梯子的顶端放于巷子一侧墙上的点C处,点C到 的距离 为b,梯子的倾斜角 为 ;将该梯子的顶端放于另一侧墙上的点D处,点D到 的距离 为c,且此时梯子的倾斜角 为 ,则 的长等于( )
A、 B、 C、 D、15. 如图,在一个宽度为 长的小巷内,一个梯子的长为a,梯子的底端位于 上的点P,将该梯子的顶端放于巷子一侧墙上的点C处,点C到 的距离 为b,梯子的倾斜角 为 ;将该梯子的顶端放于另一侧墙上的点D处,点D到 的距离 为c,且此时梯子的倾斜角 为 ,则 的长等于( )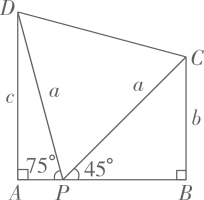 A、a B、b C、 D、c
A、a B、b C、 D、c二、填空题
-
16. 不等式 的解集是.17. 如图,已知正方形 的边长为 ,点E是边 的中点,点P是对角线 上的动点,则 的最小值是.
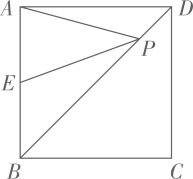 18. 关于x的一元二次方程 有一个根是 ,则k的值是.19. 一次函数 的图象与反比例函数 的图象的两个交点分别是 , ,则 .20. 如图,Rt△ABC中,∠BAC=90°,AB=6,sinC= ,以点A为圆心,AB长为半径作弧交AC于M,分别以B、M为圆心,以大于 BM长为半径作弧,两弧相交于点N,射线AN与BC相交于D,则AD的长为.
18. 关于x的一元二次方程 有一个根是 ,则k的值是.19. 一次函数 的图象与反比例函数 的图象的两个交点分别是 , ,则 .20. 如图,Rt△ABC中,∠BAC=90°,AB=6,sinC= ,以点A为圆心,AB长为半径作弧交AC于M,分别以B、M为圆心,以大于 BM长为半径作弧,两弧相交于点N,射线AN与BC相交于D,则AD的长为.
三、解答题
-
21. 计算:22. 先化简,再求值: ,其中 .23. 我国新冠疫情防控取得了阶段性胜利.学生们返校学习后,某数学兴趣小组对本校同学周末参加体育运动的情况进行抽样调查,在校园内随机抽取男女生各25人,调查情况如下表:
是否参加体育运动
男生
女生
总数
是
21
19
m
否
4
6
n
对男女生是否参加体育运动的人数绘制了条形统计图如图(1).在这次调查中,对于参加体育运动的同学,同时对其参加的主要运动项目也进行了调查,并绘制了扇形统计图如图(2).

根据以上信息解答下列问题:
(1)、 , , ;(2)、将图(1)所示的条形统计图补全;(3)、这次调查中,参加体育运动,且主要运动项目是球类的共有人;(4)、在这次调查中,共有4名男生未参加体育运动,分别是甲、乙、丙、丁四位同学,现在从他们中选出两位同学参加“我运动,我健康”的知识讲座,求恰好选出甲和乙去参加讲座的概率.(用列表或树状图解答)24. 某学校拟购进甲、乙两种规格的书柜放置新购买的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高20%,用5400元购进的甲种书柜的数量比用6300元购进乙种书柜的数量少6个.(1)、每个甲种书柜的进价是多少元?(2)、若该校拟购进这两种规格的书柜共60个,其中乙种书柜的数量不大于甲种书柜数量的 倍.该校应如何进货使得购进书柜所需费用最少?25. 如图(1),大正方形的面积可以表示为 ,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即 .同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式: .把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法” (1)、用上述“面积法”,通过如图(2)中图形的面积关系,直接写出一个多项式进行因式分解的等式:;
(1)、用上述“面积法”,通过如图(2)中图形的面积关系,直接写出一个多项式进行因式分解的等式:; (2)、如图(3), 中, , , , 是斜边 边上的高.用上述“面积法”求 的长;
(2)、如图(3), 中, , , , 是斜边 边上的高.用上述“面积法”求 的长; (3)、如图(4),等腰 中, ,点O为底边 上任意一点, , , ,垂足分别为点M,N,H,连接 ,用上述“面积法”,求证: .
(3)、如图(4),等腰 中, ,点O为底边 上任意一点, , , ,垂足分别为点M,N,H,连接 ,用上述“面积法”,求证: .

