湖北省十堰市2020年中考数学试卷
试卷更新日期:2020-08-04 类型:中考真卷
一、选择题
-
1. 的倒数是( )A、4 B、-4 C、 D、2. 某几何体的三视图如图所示,则此几何体是( )
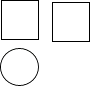 A、圆锥 B、圆柱 C、长方体 D、四棱柱3. 如图,将一副三角板重叠放在起,使直角顶点重合于点O.若 ,则 ( )
A、圆锥 B、圆柱 C、长方体 D、四棱柱3. 如图,将一副三角板重叠放在起,使直角顶点重合于点O.若 ,则 ( )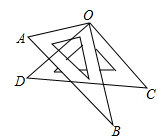 A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示:
A、 B、 C、 D、4. 下列计算正确的是( )A、 B、 C、 D、5. 一家鞋店在一段时间内销售了某种女鞋30双,各种尺码鞋的销售量如下表所示:鞋的尺码/
22
22.5
23
23.5
24
24.5
25
销售量双
1
2
5
11
7
3
1
若每双鞋的销售利润相同,则该店主最应关注的销售数据是下列统计量中的( )
A、平均数 B、方差 C、众数 D、中位数6. 已知 中,下列条件:① ;② ;③ ;④ 平分 ,其中能说明 是矩形的是( )A、① B、② C、③ D、④7. 某厂计划加工180万个医用口罩,第一周按原计划的速度生产,一周后以原来速度的1.5倍生产,结果比原计划提前一周完成任务若设原计划每周生产x万个口罩,则可列方程为( )A、 B、 C、 D、8. 如图,点 在 上, ,垂足为E.若 , ,则 ( ) A、2 B、4 C、 D、9. 根据图中数字的规律,若第n个图中出现数字396,则 ( )
A、2 B、4 C、 D、9. 根据图中数字的规律,若第n个图中出现数字396,则 ( ) A、17 B、18 C、19 D、2010. 如图,菱形 的顶点分别在反比例函数 和 的图象上,若 ,则 ( )
A、17 B、18 C、19 D、2010. 如图,菱形 的顶点分别在反比例函数 和 的图象上,若 ,则 ( )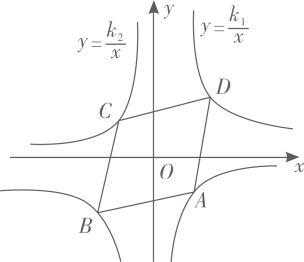 A、 B、3 C、 D、
A、 B、3 C、 D、二、填空题
-
11. 已知 ,则 .12. 如图,在 中, 是 的垂直平分线.若 , 的周长为13,则 的周长为.
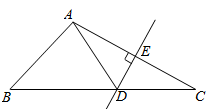 13. 某校即将举行30周年校庆,拟定了 四种活动方案,为了解学生对方案的意见,学校随机抽取了部分学生进行问卷调查(每人只能赞成一种方案),将调查结果进行统计并绘制成如下两幅不完整的统计图.若该校有学生3000人,请根据以上统计结果估计该校学生赞成方案B的人数为.
13. 某校即将举行30周年校庆,拟定了 四种活动方案,为了解学生对方案的意见,学校随机抽取了部分学生进行问卷调查(每人只能赞成一种方案),将调查结果进行统计并绘制成如下两幅不完整的统计图.若该校有学生3000人,请根据以上统计结果估计该校学生赞成方案B的人数为.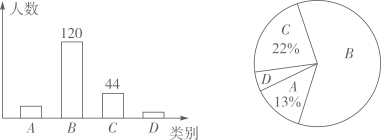 14. 对于实数 ,定义运算 .若 ,则 .15. 如图,圆心角为 的扇形 内,以 为直径作半圆,连接 .若阴影部分的面积为 ,则 .
14. 对于实数 ,定义运算 .若 ,则 .15. 如图,圆心角为 的扇形 内,以 为直径作半圆,连接 .若阴影部分的面积为 ,则 .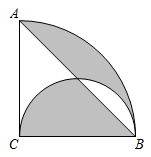 16. 如图,D是等边三角形 外一点.若 ,连接 ,则 的最大值与最小值的差为.
16. 如图,D是等边三角形 外一点.若 ,连接 ,则 的最大值与最小值的差为.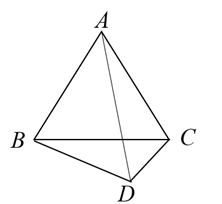
三、解答题
-
17. 计算: .18. 先化简,再求值: ,其中 .19. 如图,要想使人安全地攀上斜靠在墙面上的梯子的顶端,梯子与地面所成的角 一般要满足 ,现有一架长为 的梯子,当梯子底端离墙面 时,此时人是否能够安全使用这架梯子(参考数据: , )?
 20. 某校开展“爱国主义教育”诵读活动,诵读读本有《红星照耀中国》、《红岩》、《长征》三种,小文和小明从中随机选取一种诵读,且他们选取每一种读本的可能性相同.(1)、小文诵读《长征》的概率是;(2)、请用列表或画树状图的方法求出小文和小明诵读同一种读本的概率.21. 已知关于x的一元二次方程 有两个实数根 .(1)、求k的取值范围;(2)、若 ,求k的值.22. 如图, 为半圆O的直径,C为半圆O上一点, 与过点C的切线垂直,垂足为D, 交半圆O于点E.
20. 某校开展“爱国主义教育”诵读活动,诵读读本有《红星照耀中国》、《红岩》、《长征》三种,小文和小明从中随机选取一种诵读,且他们选取每一种读本的可能性相同.(1)、小文诵读《长征》的概率是;(2)、请用列表或画树状图的方法求出小文和小明诵读同一种读本的概率.21. 已知关于x的一元二次方程 有两个实数根 .(1)、求k的取值范围;(2)、若 ,求k的值.22. 如图, 为半圆O的直径,C为半圆O上一点, 与过点C的切线垂直,垂足为D, 交半圆O于点E.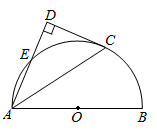 (1)、求证: 平分 ;(2)、若 ,试判断以 为顶点的四边形的形状,并说明理由.23. 某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第x天(x为整数)的生产成本为m(元台),m与x的关系如图所示.
(1)、求证: 平分 ;(2)、若 ,试判断以 为顶点的四边形的形状,并说明理由.23. 某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第x天(x为整数)的生产成本为m(元台),m与x的关系如图所示.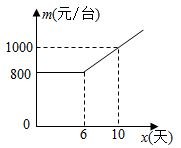 (1)、若第x天可以生产这种设备y台,则y与x的函数关系式为 , x的取值范围为;(2)、第几天时,该企业当天的销售利润最大?最大利润为多少?(3)、求当天销售利润低于10800元的天数.24. 如图1,已知 , ,点D在 上,连接 并延长交 于点F.
(1)、若第x天可以生产这种设备y台,则y与x的函数关系式为 , x的取值范围为;(2)、第几天时,该企业当天的销售利润最大?最大利润为多少?(3)、求当天销售利润低于10800元的天数.24. 如图1,已知 , ,点D在 上,连接 并延长交 于点F. (1)、猜想:线段 与 的数量关系为;(2)、探究:若将图1的 绕点B顺时针方向旋转,当 小于 时,得到图2,连接 并延长交 于点F,则(1)中的结论是否还成立?若成立,请证明;若不成立,请说明理由;(3)、拓展:图1中,过点E作 ,垂足为点G.当 的大小发生变化,其它条件不变时,若 , ,直接写出 的长.25. 已知抛物线 过点 和 ,与x轴交于另一点B,顶点为D.
(1)、猜想:线段 与 的数量关系为;(2)、探究:若将图1的 绕点B顺时针方向旋转,当 小于 时,得到图2,连接 并延长交 于点F,则(1)中的结论是否还成立?若成立,请证明;若不成立,请说明理由;(3)、拓展:图1中,过点E作 ,垂足为点G.当 的大小发生变化,其它条件不变时,若 , ,直接写出 的长.25. 已知抛物线 过点 和 ,与x轴交于另一点B,顶点为D. (1)、求抛物线的解析式,并写出D点的坐标;(2)、如图1,E为线段 上方的抛物线上一点, ,垂足为F, 轴,垂足为M,交 于点G.当 时,求 的面积;(3)、如图2, 与 的延长线交于点H,在x轴上方的抛物线上是否存在点P,使 ?若存在,求出点P的坐标:若不存在,请说明理由.
(1)、求抛物线的解析式,并写出D点的坐标;(2)、如图1,E为线段 上方的抛物线上一点, ,垂足为F, 轴,垂足为M,交 于点G.当 时,求 的面积;(3)、如图2, 与 的延长线交于点H,在x轴上方的抛物线上是否存在点P,使 ?若存在,求出点P的坐标:若不存在,请说明理由.