重庆市北碚区2020届九年级下学期数学月考试卷
试卷更新日期:2020-08-03 类型:月考试卷
一、单选题
-
1. 实数a,b在数轴上对应点的位置如图所示,则下列判断正确的是( )
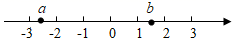 A、a>0 B、b<1 C、a<b D、a>﹣22. 如图,是由四个相同的小正方体组成的立体图形,它的主视图是( )
A、a>0 B、b<1 C、a<b D、a>﹣22. 如图,是由四个相同的小正方体组成的立体图形,它的主视图是( )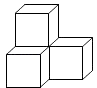 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、(x3)4=x7 B、x3•x2=x5 C、x+2x=3x2 D、x﹣2=﹣4. 下列命题正确的是( )A、过线段中点的直线上任意一点到线段两端的距离相等 B、垂直于线段的直线上任意一点到线段两端的距离相等 C、线段垂直平分线上任意一点到线段两端的距离相等 D、线段垂直平分线上的点到线段上任意两点的距离相等5. 按如图所示的运算程序,能使输出m的值为1的是( )
3. 下列计算正确的是( )A、(x3)4=x7 B、x3•x2=x5 C、x+2x=3x2 D、x﹣2=﹣4. 下列命题正确的是( )A、过线段中点的直线上任意一点到线段两端的距离相等 B、垂直于线段的直线上任意一点到线段两端的距离相等 C、线段垂直平分线上任意一点到线段两端的距离相等 D、线段垂直平分线上的点到线段上任意两点的距离相等5. 按如图所示的运算程序,能使输出m的值为1的是( )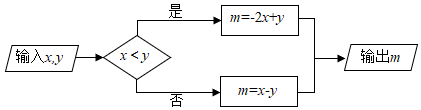 A、x=1,y=1 B、x=2,y=0 C、x=1,y=2 D、x=3,y=26. 估计 的值应在( )A、7和8之间 B、8和9之间 C、9和10之间 D、10和11之间7. 如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )
A、x=1,y=1 B、x=2,y=0 C、x=1,y=2 D、x=3,y=26. 估计 的值应在( )A、7和8之间 B、8和9之间 C、9和10之间 D、10和11之间7. 如图,AB是⊙O的直径,点P在BA的延长线上,PA=AO,PD与⊙O相切于点D,BC⊥AB交PD的延长线于点C,若⊙O的半径为1,则BC的长是( )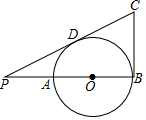 A、1.5 B、2 C、 D、8. 如图,在平面直角坐标系中,等腰Rt△ABC与等腰Rt△CDE关于原点O成位似关系,相似比为1:3,∠ACB=∠CED=90°,A,C,E是x轴正半轴上的点,B,D是第一象限的点,BC=2,则点D的坐标是( )
A、1.5 B、2 C、 D、8. 如图,在平面直角坐标系中,等腰Rt△ABC与等腰Rt△CDE关于原点O成位似关系,相似比为1:3,∠ACB=∠CED=90°,A,C,E是x轴正半轴上的点,B,D是第一象限的点,BC=2,则点D的坐标是( )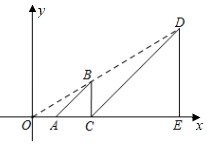 A、(9,6) B、(8,6) C、(6,9) D、(6,8)9. 如图,为加快5G网络建设,某通信公司在一个坡度i=1:2.4的山坡AB上建了一座信号塔CD,信号塔底端C到山脚A的距离AC=13米,在距山脚A水平距离18米的E处,有一高度为10米的建筑物EF,在建筑物顶端F处测得信号塔顶端D的仰角为37°(信号塔及山坡的剖面和建筑物的剖面在同一平面上),则信号塔CD的高度约是( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
A、(9,6) B、(8,6) C、(6,9) D、(6,8)9. 如图,为加快5G网络建设,某通信公司在一个坡度i=1:2.4的山坡AB上建了一座信号塔CD,信号塔底端C到山脚A的距离AC=13米,在距山脚A水平距离18米的E处,有一高度为10米的建筑物EF,在建筑物顶端F处测得信号塔顶端D的仰角为37°(信号塔及山坡的剖面和建筑物的剖面在同一平面上),则信号塔CD的高度约是( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)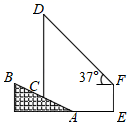 A、22.5米 B、27.5米 C、32.5米 D、45.0米10. 如图,在平面直角坐标系中,菱形ABCD的顶点B、D在反比例函数y═ (k>0)的图象上,对角线AC与BD相交于坐标原点O,若点A(﹣1,2),菱形的边长为5,则k的值是( )
A、22.5米 B、27.5米 C、32.5米 D、45.0米10. 如图,在平面直角坐标系中,菱形ABCD的顶点B、D在反比例函数y═ (k>0)的图象上,对角线AC与BD相交于坐标原点O,若点A(﹣1,2),菱形的边长为5,则k的值是( )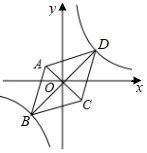 A、4 B、8 C、12 D、1611. 若数 使关于 的分式方程 有非负整数解,且使关于 的不等式组 至少有3个整数解,则符合条件的所有整数 的和是( )A、 B、 C、0 D、212. 二次函数y=ax2+bx+c(a,b,c为常数,a≠0,c>0)的自变量x与函数值y的部分对应值如表:
A、4 B、8 C、12 D、1611. 若数 使关于 的分式方程 有非负整数解,且使关于 的不等式组 至少有3个整数解,则符合条件的所有整数 的和是( )A、 B、 C、0 D、212. 二次函数y=ax2+bx+c(a,b,c为常数,a≠0,c>0)的自变量x与函数值y的部分对应值如表:x
…
﹣1
0
1
2
3
…
y=ax2+bx+c
…
p
t
n
t
0
…
有下列结论:①b>0;②关于x的方程ax2+bx+c=0的两个根是0和3;③p+2t<0;④m(am+b)≤﹣4a﹣c(m为任意实数).其中正确结论的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
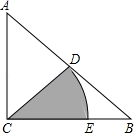
13. 计算:(3﹣π)0﹣ =.14. 代数式 有意义,则x的取值范围是.15. 如图,在Rt△ABC中,∠ACB=90°,∠A=50°,AB=10,D是AB的中点,以点C为圆心,CD长为半径画弧,交BC于点E,则图中阴影部分的面积是.(结果保留π)
 16. 点A的坐标是A(x,y),从1、2、3这三个数中任取一个数作为x的值,再从余下的两个数中任取一个数作为y的值.则点A落在直线y=﹣x+5与直线y= x及y轴所围成的封闭区域内(含边界)的概率是.17. 如图,在等腰 中, , 为 边上的高, 分别为 边上的点,将 分别沿 折叠,使点 落在 的延长线上点 处,点 落在点 处,连接 ,若 ,则 的长是.
16. 点A的坐标是A(x,y),从1、2、3这三个数中任取一个数作为x的值,再从余下的两个数中任取一个数作为y的值.则点A落在直线y=﹣x+5与直线y= x及y轴所围成的封闭区域内(含边界)的概率是.17. 如图,在等腰 中, , 为 边上的高, 分别为 边上的点,将 分别沿 折叠,使点 落在 的延长线上点 处,点 落在点 处,连接 ,若 ,则 的长是.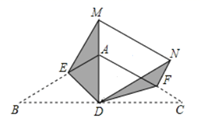 18. 如图,在平行四边形ABCD中,AB=2,∠ABC=45°,点E为射线AD上一动点,连接BE,将BE绕点B逆时针旋转60°得到BF,连接AF,则AF的最小值是.
18. 如图,在平行四边形ABCD中,AB=2,∠ABC=45°,点E为射线AD上一动点,连接BE,将BE绕点B逆时针旋转60°得到BF,连接AF,则AF的最小值是.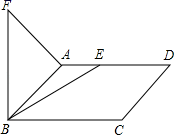
三、解答题
-
19.(1)、解方程组 .(2)、计算:(x+ )÷ .20. 如图,在平行四边形ABCD中,E、F分别是DA、BC延长线上的点,且∠ABE=∠CDF.
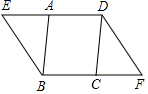
求证:
(1)、△ABE≌△CDF;(2)、四边形EBFD是平行四边形.21. 某校为提高学生体考成绩,对全校300名九年级学生进行一分种跳绳训练.为了解学生训练效果,学校体育组在九年级上学期开学初和学期末分别对九年级学生进行一分种跳绳测试,学生成绩均为整数,满分20分,大于18分为优秀.现随机抽取了同一部分学生的两次成绩进行整理、描述和分析.(成绩得分用x表示,共分成五组:A.x<13,B.13≤x<15,C.15≤x<17,D.17≤x<19,E.19≤x≤20)开学初抽取学生的成绩在D组中的数据是:17,17,17,17,17,18,18.
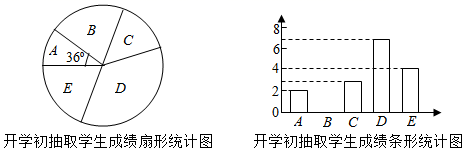
学期末抽取学生成绩统计表
学生成绩
A组
B组
C组
D组
E组
人数
0
1
4
5
a
分析数据:
平均数
中位数
众数
开学初抽取学生成绩
16
b
17
学期末抽取学生成绩
18
18.5
19
根据以上信息,解答下列问题:
(1)、直接写出图表中a、b的值,并补全条形统计图;(2)、假设该校九年级学生都参加了两次测试,估计该校学期末成绩优秀的学生人数比开学初成绩优秀的学生人数增加了多少?(3)、小莉开学初测试成绩16分,学期末测试成绩19分,根据抽查的相关数据,请选择一个合适的统计量评价小莉的训练效果.22. 某数学小组对函数y1= 图象和性质进行探究.当x=4时,y1=0. (1)、当x=5时,求y1的值;(2)、在给出的平面直角坐标系中,补全这个函数的图象,并写出这个函数的一条性质;(3)、进一步探究函数图象并解决问题:已知函数y2=﹣ 的图象如图所示,结合函数y1的图象,直接写出不等式y1≥y2的解集.23. 某商场销售A、B两种新型小家电,A型每台进价40元,售价50元,B型每台进价32元,售价40元,4月份售出A型40台,且销售这两种小家电共获利不少于800元.(1)、求4月份售出B型小家电至少多少台?(2)、经市场调查,5月份A型售价每降低1元,销量将增加10台;B型售价每降低1元,销量将在4月份最低销量的基础上增加15台.为尽可能让消费者获得实惠,商场计划5月份A、B两种小家电都降低相同价格,且希望销售这两种小家电共获利965元,则这两种小家电都应降低多少元?24. 对任意一个两位数m,如果m等于两个正整数的平方和,那么称这个两位数m为“平方和数”,若m=a2+b2(a、b为正整数),记A(m)=ab.例如:29=22+52 , 29就是一个“平方和数”,则A(29)=2×5=10.(1)、判断25是否是“平方和数”,若是,请计算A(25)的值;若不是,请说明理由;(2)、若k是一个“平方和数”,且A(k)= ,求k的值.25. 如图,一个二次函数的图象经过点A(0,1),它的顶点为B(1,3).
(1)、当x=5时,求y1的值;(2)、在给出的平面直角坐标系中,补全这个函数的图象,并写出这个函数的一条性质;(3)、进一步探究函数图象并解决问题:已知函数y2=﹣ 的图象如图所示,结合函数y1的图象,直接写出不等式y1≥y2的解集.23. 某商场销售A、B两种新型小家电,A型每台进价40元,售价50元,B型每台进价32元,售价40元,4月份售出A型40台,且销售这两种小家电共获利不少于800元.(1)、求4月份售出B型小家电至少多少台?(2)、经市场调查,5月份A型售价每降低1元,销量将增加10台;B型售价每降低1元,销量将在4月份最低销量的基础上增加15台.为尽可能让消费者获得实惠,商场计划5月份A、B两种小家电都降低相同价格,且希望销售这两种小家电共获利965元,则这两种小家电都应降低多少元?24. 对任意一个两位数m,如果m等于两个正整数的平方和,那么称这个两位数m为“平方和数”,若m=a2+b2(a、b为正整数),记A(m)=ab.例如:29=22+52 , 29就是一个“平方和数”,则A(29)=2×5=10.(1)、判断25是否是“平方和数”,若是,请计算A(25)的值;若不是,请说明理由;(2)、若k是一个“平方和数”,且A(k)= ,求k的值.25. 如图,一个二次函数的图象经过点A(0,1),它的顶点为B(1,3).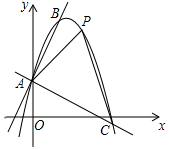 (1)、求这个二次函数的表达式;(2)、过点A作AC⊥AB交抛物线于点C,点P是直线AC上方抛物线上的一点,当△APC面积最大时,求点P的坐标和△APC的面积最大值.26. 如图1,在正方形 中,对角线 相交于点 ,点 为线段 上一点,连接 ,将 绕 点顺时针旋转 得到 ,连接 交 于点 .
(1)、求这个二次函数的表达式;(2)、过点A作AC⊥AB交抛物线于点C,点P是直线AC上方抛物线上的一点,当△APC面积最大时,求点P的坐标和△APC的面积最大值.26. 如图1,在正方形 中,对角线 相交于点 ,点 为线段 上一点,连接 ,将 绕 点顺时针旋转 得到 ,连接 交 于点 .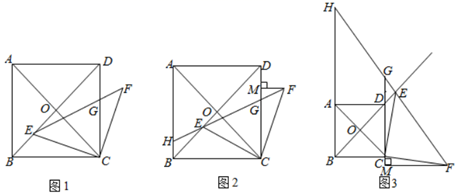 (1)、若 ,求 的面积;(2)、如图2,线段 的延长线交 于点 ,过点 作 于点 ,求证: ;(3)、如图3,点 为射线 上一点,线段 的延长线交直线 于点 ,交直线 于点 ,过点 作 垂直直线 于点 ,请直接写出线段 的数量关系.
(1)、若 ,求 的面积;(2)、如图2,线段 的延长线交 于点 ,过点 作 于点 ,求证: ;(3)、如图3,点 为射线 上一点,线段 的延长线交直线 于点 ,交直线 于点 ,过点 作 垂直直线 于点 ,请直接写出线段 的数量关系.