初中数学人教版七年级上学期 第四章 几何图形初步
试卷更新日期：2020-08-03 类型：单元试卷
一、单选题
-
1. 如图所示，直线AB上有一点C，过点C作CD⊥CE，那么图中∠1和∠2的关系是（ ）
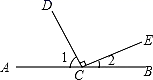A、对顶角 B、同位角 C、互为补角 D、互为余角2. 下列图形中的两个角互为补角的是（ ）
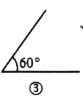
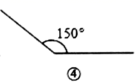A、①和② B、①和③ C、①和④ D、③和④3. 如图所示，∠1=20°，∠AOB=90°，点C、O、D在同一直线上，则∠2的度数为（ ）
A、70° B、80° C、160° D、110°4. 如图所示，下列说法错误的是（ ）
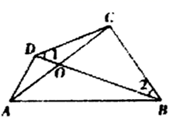A、 也可用 表示 B、 也可用 表示 C、 也可用 表示 D、 也可用 表示5. 下列说法：其中正确的是（ ）①若∠A+∠B＝180°，则∠A，∠B互补；
②若∠A+∠B＝180°，则∠A，∠B是同旁内角；
③若∠A，∠B互补，则∠A+∠B＝180°；
④若∠A，∠B是同旁内角，则∠A+∠B＝180°.
A、①②③④ B、①③ C、①③④ D、①②③6. 如图，点E，F分别是AB，CD的中点，AB：BC：CD=2：3：4，若EF=18，则AD的长为（ ）
A、24 B、27 C、32 D、367. 如图，轮船航行到C处时，观测到小岛B的方向是北偏西 ，那么同时从B观测轮船的方向是（ ）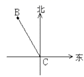
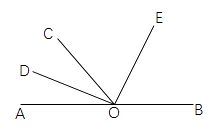
A、南偏西 B、东偏西 C、南偏东 D、南偏东8. 一个正方体的六个面上分别标有-1，-2，-3，-4，-5，-6中的一个数，各个面上所标数字都不相同，如图是这个正方体的三种放置方法，则数字-3对面的数字是（ ）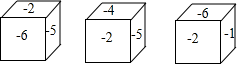
A、-1 B、-2 C、-5 D、-69. 如图，已知A，O，B在一条直线上，∠1是锐角，则∠1的余角是（ ）
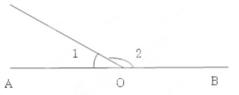A、 B、 C、 D、∠2-∠110. 如图，C、D是线段AB上两点，M、N分别是线段AD、BC的中点，下列结论：①若AD=BM，则AB=3BD；②若AC=BD，则AM=BN；③AC-BD=2（MC-DN）；④2MN=AB-CD．其中正确的结论是（ ）
A、①②③ B、③④ C、①②④ D、①②③④二、填空题
-
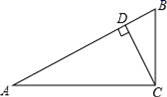
11. 如图，△ABC中，∠ACB=90°，CD⊥AB于点D，则点B到直线CD的距离是线段的长．
12. 已知一个角的余角是它的补角的 ，则这个角为 ．13. ， ，14. 2019年10月1日，阅兵空中梯队战机通过北京天安门广场上空时，其尾部拉出五彩斑斓的线，庆祝我们伟大的祖国成立70周年.飞机表演“飞机拉线”，可以用数学知识解释为.15. 随着我国的发展与强大，中国文化与世界各国文化的交流和融合进一步加强，各国学校之间的交流活动逐年增加，在与国际友好学校交流活动中，小敏打算制作一个正方体礼盒送给外国朋友，每个面上分别书写一种中华传统美德，一共有“仁义礼智信孝”六个字，如图是她设计的礼盒平面展开图，那么“礼”字对面的字是.
16. 26.54°=°′″．17. 若 与 互为补角， ， ，且 ，则 的余角的度数是度.（结果用同时含m ， n的代数式表示）18. 已知点A，B，C都在直线l上，点P是线段AC的中点.设 ， ，则线段BC的长为（用含a，b的代数式表示）19. 如图所示，将长方形纸片ABCD进行折叠，如果∠BHG=70°，那么∠BHE=度．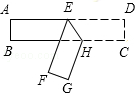
20. 如图，在数轴上，点A，B分别表示-15，9，点P，Q分别从点A，B同时开始沿数轴正方向运动，点P的速度是每秒3个单位，点Q的速度是每秒1个单位，运动时间为t秒．在运动过程中，当点P，点Q和原点O这三点中的一点恰好是另外两点为端点的线段的中点时，t的值是 ．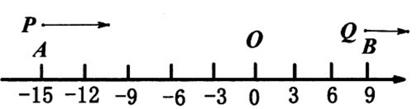
三、解答题
-
21. 写出下图中各个几何体的名称，并按锥体和柱体把它们分类．
22. 如图B、C两点把线段AD分成2：3：4三部分，M是AD的中点，CD=8，求MC的长．
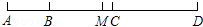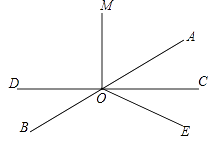
23. 如图，已知2∠BOC=∠AOC，∠AOC的余角比∠BOC小30°，作射线OD，使得∠AOC=4∠AOD，求∠DOB的度数．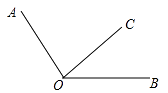
24. 如图，已知直线AB与CD交于点O，OM⊥CD，OA平分∠MOE，且∠BOD＝28°，求∠AOM，∠COE的度数．
