江苏省扬中市2020届九年级下学期数学5月月考试卷
试卷更新日期:2020-08-03 类型:月考试卷
一、填空题
-
1. 数-2020的绝对值是 .2. 分解因式: .3. 新型冠状病毒感染的肺炎病例在武汉出现后,2020年1月12日,世界卫生组织正式将造成武汉肺炎疫情的新型冠状病毒命名为“2019新型冠状病毒”(2019-nCoV),据科学家研究发现,该病毒毒株仅为0.000000098m,则数据0.000000098用科学记数法应表示为.4. 使 有意义的x的取值范围是.5. 农科院对甲、乙两种甜玉米各10块试验田进行试验后,得到甲、乙两个品种每公顷的平均产量相同,而甲、乙两个品种产量的方差分别为
 ,
,  ,则产量较为稳定的品种是(填“甲”或“乙”). 6. 如图,已知 , , ,则 的度数为.
,则产量较为稳定的品种是(填“甲”或“乙”). 6. 如图,已知 , , ,则 的度数为. 7. 如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,指针落在阴影部分的概率为.
7. 如图,转盘中6个扇形的面积都相等.任意转动转盘1次,当转盘停止转动时,指针落在阴影部分的概率为. 8. 如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是.
8. 如图,四边形ABCD是⊙O的内接四边形,若∠DAB=60°,则∠BCD的度数是.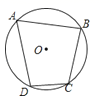 9. 已知圆锥的底面圆半径为 ,高为 ,则圆锥的侧面积是 .10. 如图,菱形 的边长为15, ,则 .
9. 已知圆锥的底面圆半径为 ,高为 ,则圆锥的侧面积是 .10. 如图,菱形 的边长为15, ,则 . 11. 已知点 与点 的坐标,抛物线 与线段 有交点,则 的取值范围是.12. 如图,在平面直角坐标系中,直线 交 轴于点 ,现将直线 绕点 顺时针方向旋转45°交 轴于点 ,则直线 的函数表达式是.
11. 已知点 与点 的坐标,抛物线 与线段 有交点,则 的取值范围是.12. 如图,在平面直角坐标系中,直线 交 轴于点 ,现将直线 绕点 顺时针方向旋转45°交 轴于点 ,则直线 的函数表达式是.
二、单选题
-
13. 下列计算正确的是( )A、 B、 C、 D、14. 如图是由6个小正方体搭成的物体,该所示物体的主视图是( )
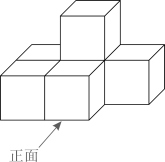 A、
A、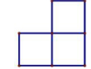 B、
B、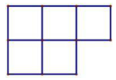 C、
C、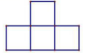 D、
D、 15. 某校组织“国学经典”诵读比赛,参赛10名选手的得分情况如下表所示:
15. 某校组织“国学经典”诵读比赛,参赛10名选手的得分情况如下表所示:分数/分
85
88
91
94
人数/人
2
3
4
1
那么,这10名选手得分的中位数和众数分别是( )
A、88和91 B、91和89.5 C、91和91 D、89.5和9116. 古代名著《算学启蒙》中有一题:良马日行二百二十里,驽马日行一百四十里,驽马先行一十二日,问良马几何追及之.意思是:跑得快的马每天走220里,跑得慢的马每天走140里.慢马先走12天,快马几天可追上慢马?若设快马 天可追上慢马,则由题意,可列方程为( )A、 B、 C、 D、17. 如图,在平面直角坐标系中,已知点A(-3,6)、B(-9,-3),以原点O为位似中心,相似比为 ,把△ABO缩小,则点A的对应点A′的坐标是( ) A、(-1,2) B、(-9,18) C、(-9,18)或(9,-18) D、(-1,2)或(1,-2)18. 如图,已知 , 为线段 上的一个动点,分别以 , 为边在 的同侧作菱形 和菱形 ,点 , , 在一条直线上, . , 分别是对角线 , 的中点.当点 在线段 上移动时,点 , 之间的距离最短为( )
A、(-1,2) B、(-9,18) C、(-9,18)或(9,-18) D、(-1,2)或(1,-2)18. 如图,已知 , 为线段 上的一个动点,分别以 , 为边在 的同侧作菱形 和菱形 ,点 , , 在一条直线上, . , 分别是对角线 , 的中点.当点 在线段 上移动时,点 , 之间的距离最短为( )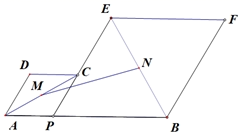 A、 B、 C、4 D、3
A、 B、 C、4 D、3三、解答题
-
19.(1)、计算:(2)、化简:20.(1)、解方程:(2)、解不等式组:21. 如图,四边形 中,对角线 、 交于点 , ,点 是 上一点,且 , .
 (1)、求证: ;(2)、若 ,求 的度数.22. 有三个质地、大小都相同的小球分别标上数字2,-1,3后放入一个不透明的口袋搅匀,任意摸出一个小球,记下数字 后,放回口袋中搅匀,再任意摸出一个小球,又记下数字b.这样就得到一个点的坐标 .(1)、求这个点 恰好在函数 的图像上的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)(2)、如果再往口袋中增加 个标上数字2的小球,按照同样的操作过程,所得到的点 恰好在函数 的图像上的概率是(请用含 的代数式直接写出结果).23. 某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市16000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
(1)、求证: ;(2)、若 ,求 的度数.22. 有三个质地、大小都相同的小球分别标上数字2,-1,3后放入一个不透明的口袋搅匀,任意摸出一个小球,记下数字 后,放回口袋中搅匀,再任意摸出一个小球,又记下数字b.这样就得到一个点的坐标 .(1)、求这个点 恰好在函数 的图像上的概率.(请用“画树状图”或“列表”等方法给出分析过程,并求出结果)(2)、如果再往口袋中增加 个标上数字2的小球,按照同样的操作过程,所得到的点 恰好在函数 的图像上的概率是(请用含 的代数式直接写出结果).23. 某课题组为了解全市九年级学生对数学知识的掌握情况,在一次数学检测中,从全市16000名九年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
请根据以上图表提供的信息,解答下列问题:
(1)、随机抽取部分学生的总人数是人,表格中的 .(2)、请补全频数分布直方图;(3)、如果把成绩在90分以上(含90分)定为优秀,那么该市16000名九年级考生数学成绩为优秀的学生约有多少名?24. 如图,某中学数学活动小组在学习了“利用三角函数测高”后,选定测量小河对岸一幢建筑物 的高度,他们先在斜坡上的 处,测得建筑物顶端 的仰角为30°.且 离地面的高度 .坡底 ,然后在 处测得建筑物顶端 的仰角是60°,点 、 、 在同一水平线上,求建筑物 的高.(结果用含有根号的式子表示)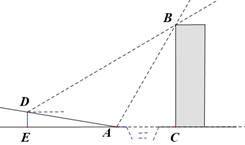 25. 如图,直线 : 与 轴、 轴交于 、 两点,与反比例函数 的图像交于点 ,且 .
25. 如图,直线 : 与 轴、 轴交于 、 两点,与反比例函数 的图像交于点 ,且 . (1)、求反比例函数的解析式;(2)、点 是直线 上一点,过点 作 轴的平行线交反比例函数 和 的图像于 , 两点,连 , ,当 时,求 的值.26. 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)、求反比例函数的解析式;(2)、点 是直线 上一点,过点 作 轴的平行线交反比例函数 和 的图像于 , 两点,连 , ,当 时,求 的值.26. 如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD. (1)、求证:CD2=CA•CB;(2)、求证:CD是⊙O的切线;(3)、过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA= ,求BE的长.27. 已知,在平面直角坐标系中, 为坐标原点,抛物线 分别交 轴于 、 两点(点 在点 的侧),与 轴交于点 ,连接 , .(1)、如图1,求 的值;
(1)、求证:CD2=CA•CB;(2)、求证:CD是⊙O的切线;(3)、过点B作⊙O的切线交CD的延长线于点E,若BC=12,tan∠CDA= ,求BE的长.27. 已知,在平面直角坐标系中, 为坐标原点,抛物线 分别交 轴于 、 两点(点 在点 的侧),与 轴交于点 ,连接 , .(1)、如图1,求 的值; (2)、如图2, 是 轴上一点(不与点 、 重合),过点 作 轴的平行线,交抛物线于点 ,交直线 于点 .
(2)、如图2, 是 轴上一点(不与点 、 重合),过点 作 轴的平行线,交抛物线于点 ,交直线 于点 .
①当点 在点 右侧时,连接AF,当 时,求 的长.
②当点 在运动时,若 、 、 中有两条线段相等,求此时点 的坐标.
 28. 如图1所示是小明设计的带菱形图案的花边作品,该作品由形如图2所示的矩形图案拼接而成(不重叠,无缝隙),小明发现图(2)具有对称之美,它既是轴对称图形,也是中心对称图形,并对这个图形进行探究.
28. 如图1所示是小明设计的带菱形图案的花边作品,该作品由形如图2所示的矩形图案拼接而成(不重叠,无缝隙),小明发现图(2)具有对称之美,它既是轴对称图形,也是中心对称图形,并对这个图形进行探究. (1)、如图3,若知图案的一部分,请你根据如图2将图3的图案补充完整(要求:尺规作图,保留作图痕迹,不写作法);
(1)、如图3,若知图案的一部分,请你根据如图2将图3的图案补充完整(要求:尺规作图,保留作图痕迹,不写作法); (2)、如图4, , ,上、下两个阴影部分的面积之和为 ,其内部菱形由两组距离相等的平行线两两相交得到,求该菱形的周长;
(2)、如图4, , ,上、下两个阴影部分的面积之和为 ,其内部菱形由两组距离相等的平行线两两相交得到,求该菱形的周长; (3)、小明认为:图4中的4个空白部分在一定条件下能拼成一个正方形(不重叠,无缝隙),请你帮助小明写出应满足的条件(提示:求出 与 的长度之比,并指出点 、 的位置).
(3)、小明认为:图4中的4个空白部分在一定条件下能拼成一个正方形(不重叠,无缝隙),请你帮助小明写出应满足的条件(提示:求出 与 的长度之比,并指出点 、 的位置).