湖北省宜昌市五峰土家族自治县2020届九年级下学期数学第一次大联考试卷
试卷更新日期:2020-08-03 类型:中考模拟
一、单选题
-
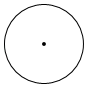
1. 有理数 的倒数为( ).A、 B、 C、 D、2. 如图是下面哪个图形的俯视图( )
 A、
A、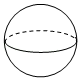 B、
B、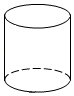 C、
C、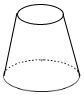 D、
D、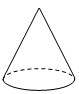 3. 掷一枚质地均匀的硬币10次,下列说法正确的是( )A、必有5次正面朝上 B、可能有5次正面朝上 C、掷2次必有1次正面朝上 D、不可能10次正面朝上4. 自然界中的数学不胜枚举,如蜜蜂建造的蜂房既坚固又省料,其厚度为0.000073米,将0.000073用科学记数法表示为( ).A、73×10﹣6 B、0.73×10﹣4 C、7.3×10﹣5 D、7.3×10﹣45. 下列四个图形中,既是轴对称图形,又是中心对称图形的是( ).A、
3. 掷一枚质地均匀的硬币10次,下列说法正确的是( )A、必有5次正面朝上 B、可能有5次正面朝上 C、掷2次必有1次正面朝上 D、不可能10次正面朝上4. 自然界中的数学不胜枚举,如蜜蜂建造的蜂房既坚固又省料,其厚度为0.000073米,将0.000073用科学记数法表示为( ).A、73×10﹣6 B、0.73×10﹣4 C、7.3×10﹣5 D、7.3×10﹣45. 下列四个图形中,既是轴对称图形,又是中心对称图形的是( ).A、 B、
B、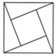 C、
C、 D、
D、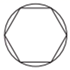 6. 如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于M、N两点,作直线MN , 交BC于点D , 连接AD , 则∠CAD的度数是( )
6. 如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于M、N两点,作直线MN , 交BC于点D , 连接AD , 则∠CAD的度数是( )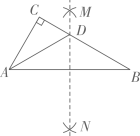 A、20° B、30° C、45° D、60°7. 下列运算正确的是( )A、m2•m3=m6 B、(m4)2=m6 C、m3+m3=2m3 D、(m﹣n)2=m2﹣n28. 某班40名同学一周参加体育锻炼时间统计如表所示:
A、20° B、30° C、45° D、60°7. 下列运算正确的是( )A、m2•m3=m6 B、(m4)2=m6 C、m3+m3=2m3 D、(m﹣n)2=m2﹣n28. 某班40名同学一周参加体育锻炼时间统计如表所示:人数(人)
3
17
13
7
时间(小时)
7
8
9
10
那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A、17,8.5 B、17,9 C、8,9 D、8,8.59. 如图,数轴的单位长度为1,如果点 表示的数是-1,那么点 表示的数是( ). A、0 B、1 C、2 D、310. 如图,已知圆心角∠BOC=100°, 则圆周角∠BAC为 ( ).
A、0 B、1 C、2 D、310. 如图,已知圆心角∠BOC=100°, 则圆周角∠BAC为 ( ).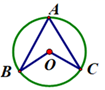 A、25° B、50° C、100° D、200°11. 二次函数y=ax2+b(b>0)与反比例函数 y= 在同一坐标系中的图象可能是( )
A、25° B、50° C、100° D、200°11. 二次函数y=ax2+b(b>0)与反比例函数 y= 在同一坐标系中的图象可能是( )
A、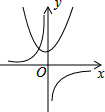 B、
B、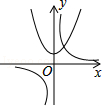 C、
C、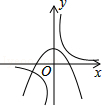 D、
D、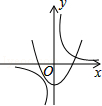
二、填空题
-
12. 若分式 有意义,则 的取值范围是 .13. 定义a*b=ab+a+b,若3*x=27,则x的值是。14. 把一块含有 角的直角三角板与两条长边平行的直尺如图放置(直角顶点在直尺的一条长边上).若 ,则 .
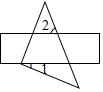 15. 如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0, ).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是.
15. 如图,已知一个直角三角板的直角顶点与原点重合,另两个顶点A,B的坐标分别为(-1,0),(0, ).现将该三角板向右平移使点A与点O重合,得到△OCB′,则点B的对应点B′的坐标是.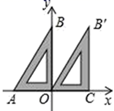
三、解答题
-
16. 先化简,再求值:x(x+2)-(x+1)(x-1),其中x=- .17. 解不等式组 ,并把解集在数轴上表示出来.
 18. 如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F.
18. 如图,在△ABC中,AD是BC边上的中线,E是AB边上一点,过点C作CF∥AB交ED的延长线于点F. (1)、求证:△BDE≌△CDF;(2)、当AD⊥BC,AE=1,CF=2时,求AC的长.19. 密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知气体的密度ρ与体积V是反比例函数关系,它的图象如图所示.
(1)、求证:△BDE≌△CDF;(2)、当AD⊥BC,AE=1,CF=2时,求AC的长.19. 密闭容器内有一定质量的二氧化碳,当容器的体积V(单位:m3)变化时,气体的密度ρ(单位:kg/m3)随之变化,已知气体的密度ρ与体积V是反比例函数关系,它的图象如图所示. (1)、求密度ρ关于体积V的函数解析式;(2)、当V=9m3时,求二氧化碳的密度ρ.20. 为了解阳光社区20~60岁居民购物最喜欢的支付方式,该兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
(1)、求密度ρ关于体积V的函数解析式;(2)、当V=9m3时,求二氧化碳的密度ρ.20. 为了解阳光社区20~60岁居民购物最喜欢的支付方式,该兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题: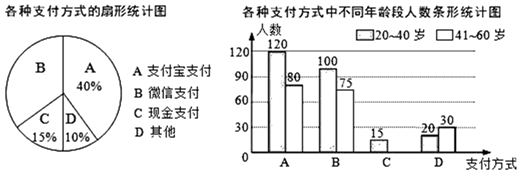 (1)、求参与问卷调查的总人数.(2)、补全条形统计图.(3)、该社区中20~60岁的居民约5000人,估算这些人中最喜欢微信支付方式的人数.21. 如图,在△ABC中,∠BAC=90°,点E在BC边上,且CA=CE,过A,C,E三点的⊙O交AB于另一点F,作直径AD,连结DE并延长交AB于点G,连结CD,CF.
(1)、求参与问卷调查的总人数.(2)、补全条形统计图.(3)、该社区中20~60岁的居民约5000人,估算这些人中最喜欢微信支付方式的人数.21. 如图,在△ABC中,∠BAC=90°,点E在BC边上,且CA=CE,过A,C,E三点的⊙O交AB于另一点F,作直径AD,连结DE并延长交AB于点G,连结CD,CF.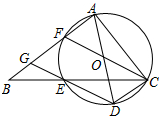 (1)、求证:四边形DCFG是平行四边形;(2)、当BE=4,CD= AB时,求⊙O的直径长.22. 今年受新冠病毒疫情的影响,王大伯家的两种水果“沃柑”和“夏橙”存在销售困难,这一情况被住村干部得知后,决定帮助王大伯提供线上(网上销售)和线下(批发给店铺)两种形式销售.通过一个星期的销售,其中通过线上销售1600斤,且通过线上销售的斤数比线下销售的斤数多60%.(1)、求王大伯的一星期线上线下销售“沃柑”和“夏橙”一共多少斤?(2)、如果销售的这些水果中“沃柑”比“夏橙”的2倍少700斤,而通过线上销售的“夏橙”的斤数不小于线下销售“夏橙”的2倍,则通过线下销售的“沃柑”至少多少斤?23. 如图1,在边长为1的正方形ABCD中,动点E,F分别在边AB,CD上,将正方形ABCD沿直线EF折叠,使点B的对应点M始终落在边AD上(点M不与点A,D重合),点C落在点N处,MN与CD交于点P,设BE=x.
(1)、求证:四边形DCFG是平行四边形;(2)、当BE=4,CD= AB时,求⊙O的直径长.22. 今年受新冠病毒疫情的影响,王大伯家的两种水果“沃柑”和“夏橙”存在销售困难,这一情况被住村干部得知后,决定帮助王大伯提供线上(网上销售)和线下(批发给店铺)两种形式销售.通过一个星期的销售,其中通过线上销售1600斤,且通过线上销售的斤数比线下销售的斤数多60%.(1)、求王大伯的一星期线上线下销售“沃柑”和“夏橙”一共多少斤?(2)、如果销售的这些水果中“沃柑”比“夏橙”的2倍少700斤,而通过线上销售的“夏橙”的斤数不小于线下销售“夏橙”的2倍,则通过线下销售的“沃柑”至少多少斤?23. 如图1,在边长为1的正方形ABCD中,动点E,F分别在边AB,CD上,将正方形ABCD沿直线EF折叠,使点B的对应点M始终落在边AD上(点M不与点A,D重合),点C落在点N处,MN与CD交于点P,设BE=x. (1)、当AM= 时,求x的值;(2)、如图2,连接BM、过B点作BH⊥MN,垂足为H,求证:BM是∠ABH的角平分线;(3)、随着点M在边AD上位置的变化,△PDM的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值;(4)、设四边形BEFC的面积为S,求S与x之间的函数表达式,并求出S的最小值.24. 如图,在平面直角坐标系xOy中,直线y=mx+k,与x轴,y轴分别交于点A,B,经过点A的抛物线y=ax2+bx﹣3a与x轴另一个交点为点D,AD=4,将点B向右平移5个单位长度,得到点C.
(1)、当AM= 时,求x的值;(2)、如图2,连接BM、过B点作BH⊥MN,垂足为H,求证:BM是∠ABH的角平分线;(3)、随着点M在边AD上位置的变化,△PDM的周长是否发生变化?如变化,请说明理由;如不变,请求出该定值;(4)、设四边形BEFC的面积为S,求S与x之间的函数表达式,并求出S的最小值.24. 如图,在平面直角坐标系xOy中,直线y=mx+k,与x轴,y轴分别交于点A,B,经过点A的抛物线y=ax2+bx﹣3a与x轴另一个交点为点D,AD=4,将点B向右平移5个单位长度,得到点C.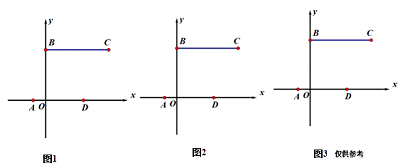 (1)、求点C的坐标(用k表示);(2)、求抛物线的对称轴;(3)、若抛物线的对称轴在y轴右侧,连接BD,BD比BO长1,抛物线与线段BC恰有一个公共点,求直线y=mx+k的解析式和a的取值范围.
(1)、求点C的坐标(用k表示);(2)、求抛物线的对称轴;(3)、若抛物线的对称轴在y轴右侧,连接BD,BD比BO长1,抛物线与线段BC恰有一个公共点,求直线y=mx+k的解析式和a的取值范围.