湖北省武汉市汉阳区2020届九年级下学期数学5月月考试卷
试卷更新日期:2020-08-03 类型:月考试卷
一、单选题
-
1. 下列各数中,比﹣2小的数是( )A、﹣3 B、﹣1 C、0 D、12. 式子 在实数范围内有意义,则 的取值范围是( )A、 B、 C、 D、3. 不透明的袋子中只有4个黑球和2个白球,这些球除颜色外无其他差别,随机从袋子中一次摸出3个球,下列事件是不可能事件的是( )A、3个球都是黑球 B、3个球都是白球 C、三个球中有黑球 D、3个球中有白球4. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性,下列美术字是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,下列选项中不是正六棱柱的三视图的是( )
5. 如图,下列选项中不是正六棱柱的三视图的是( )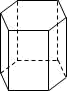 A、
A、 B、
B、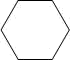 C、
C、 D、
D、 6. 已知小明从 地到 地,速度为 千米/小时, 两地相距 千米,若用 (小时)表示行走的时间, (千米)表示余下的路程,则 与 之间的函数表达式是( )A、 B、 C、 D、7. 疫情防控,我们一直在坚守.某居委会组织两个检查组,分别对“居民体温”和“居民安全出行”的情况进行抽查.若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查,则他们恰好抽到同一个小区的概率是( )A、 B、 C、 D、8. 已知反比例函数 两点在该图象上.下列命题:①该图象 分别位于第二、第四象限;②过 作 轴, 为垂足,连接 ,则 的面积为 ; ③若 ,则 ;④若 ,则 其中真命题个数是( )A、 B、 C、 D、9. 如图,在 上依次有 三点, 的延长线交 于 , 过点 作 交 的延长线于 交 于点 .连接 , 若 且 ,则劣弧 的长是( )
6. 已知小明从 地到 地,速度为 千米/小时, 两地相距 千米,若用 (小时)表示行走的时间, (千米)表示余下的路程,则 与 之间的函数表达式是( )A、 B、 C、 D、7. 疫情防控,我们一直在坚守.某居委会组织两个检查组,分别对“居民体温”和“居民安全出行”的情况进行抽查.若这两个检查组在辖区内的某三个校区中各自随机抽取一个小区进行检查,则他们恰好抽到同一个小区的概率是( )A、 B、 C、 D、8. 已知反比例函数 两点在该图象上.下列命题:①该图象 分别位于第二、第四象限;②过 作 轴, 为垂足,连接 ,则 的面积为 ; ③若 ,则 ;④若 ,则 其中真命题个数是( )A、 B、 C、 D、9. 如图,在 上依次有 三点, 的延长线交 于 , 过点 作 交 的延长线于 交 于点 .连接 , 若 且 ,则劣弧 的长是( ) A、 B、 C、 D、10. 设 都是整数,且每个数都满足 都满足 ,若 的最小值是 的最小值是 ,...,则 的最小值是( )A、 B、 C、 D、
A、 B、 C、 D、10. 设 都是整数,且每个数都满足 都满足 ,若 的最小值是 的最小值是 ,...,则 的最小值是( )A、 B、 C、 D、二、填空题
-
11. 计算 的结果是 .12. 已知小明最近几次数学考试的成绩分别为: .则这组数据的中位数是.13. 计算 结果是.14. 如图, 为平行四边形 边 上一点,将 沿 翻折得到 , 点 在 上,且 ,若 ,则 .
 15. 如图,二次函数y=ax2+bx+c(a≠0)图象与x轴交于A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(不包括这两个点),下列结论:
15. 如图,二次函数y=ax2+bx+c(a≠0)图象与x轴交于A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(不包括这两个点),下列结论:①当﹣1<x<3时,y>0;②﹣1<a<﹣ ;③当m≠1时,a+b>m(am+b);④4ac﹣b2>8a其中正确的结论是.
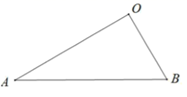
 16. 问题背景:如图 1,在 和 中, ,连接 交 的延长线于点 .则 的值是.
16. 问题背景:如图 1,在 和 中, ,连接 交 的延长线于点 .则 的值是.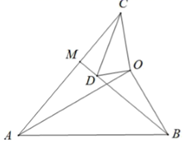
问题解决:如图 2,在问题背景的条件下,将 绕点 在平面内旋转,点 始终在 的外部, 所在直线交于点 ,若 ,当点 与点 重合时, 的长是
三、解答题
-
17. 计算:18. 如图, 于点 于点 , 求证: .
 19. “微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了某市 名教师某日“微信运动”中的步数情况并进行统计整理,绘制了如下的统计图表(不完整):
19. “微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了某市 名教师某日“微信运动”中的步数情况并进行统计整理,绘制了如下的统计图表(不完整):请根据以上信息,解答下列问题
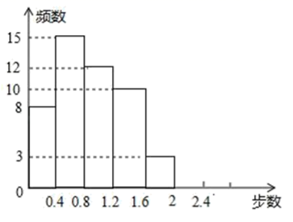 (1)、写出 的值;(2)、补全频数分布直方图;(3)、若该市约有 名教师,估计日行走步数超过 万步(包含 万步)的教师约有多少名?
(1)、写出 的值;(2)、补全频数分布直方图;(3)、若该市约有 名教师,估计日行走步数超过 万步(包含 万步)的教师约有多少名?步数(万步)
频数
频率
20. 如图,在每个小正方形边长为 的网格中, 的顶点 均在格点上, 是以 为圆心, 为半径的一段圆弧,请用无刻度的直尺画图(保留连线痕迹).(1)、 的长为;(2)、将线段 绕点 逆时针旋转得到 ,旋转角为 ( ),连接 .①如图1,若 是 的中点,请在网格中画出 ,使 ;
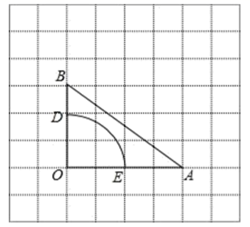
②如图2,连接 ,请在网格中画出点 ,使 的值最小.
 21. 如图, 内接于 , ,直径 与 相交于点 ,过点 作 垂足为 ,延长 交 的延长线于点 ,连接 .
21. 如图, 内接于 , ,直径 与 相交于点 ,过点 作 垂足为 ,延长 交 的延长线于点 ,连接 . (1)、求证: 与 相切;(2)、若 ,且 ,求 的长22. 商店销售某上市新品,期间共销售该产品 天,设销售时间为 天,第一天销售单价定为 元/千克,售出 千克.从第 天至第 天,该产品成本价为 元/千克,销售单价每天降低 元,销售量每天增加 千克.从第 天开始,成本价降为 元/千克,销售单价稳定在 元/千克,每天销售量 (千克)与第 天满足一次函数关系 ,设第 天销售利润为 元(1)、直接写出 与 的函数关系式;(2)、问销售该商品第几天时,当天销售利润最大,最大利润是多少?(3)、该商品在这 天的销售过程中,共有多少天每天销售利润不低于 元?23. 如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)、求证: 与 相切;(2)、若 ,且 ,求 的长22. 商店销售某上市新品,期间共销售该产品 天,设销售时间为 天,第一天销售单价定为 元/千克,售出 千克.从第 天至第 天,该产品成本价为 元/千克,销售单价每天降低 元,销售量每天增加 千克.从第 天开始,成本价降为 元/千克,销售单价稳定在 元/千克,每天销售量 (千克)与第 天满足一次函数关系 ,设第 天销售利润为 元(1)、直接写出 与 的函数关系式;(2)、问销售该商品第几天时,当天销售利润最大,最大利润是多少?(3)、该商品在这 天的销售过程中,共有多少天每天销售利润不低于 元?23. 如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”. (1)、若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B=°;(2)、如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.(3)、如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.24. 如图1,直线 与 轴, 轴分别交于点 ,点 ,抛物线 经过点 ,点 和点 ,并与直线 交于另一点 .
(1)、若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B=°;(2)、如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.(3)、如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.24. 如图1,直线 与 轴, 轴分别交于点 ,点 ,抛物线 经过点 ,点 和点 ,并与直线 交于另一点 .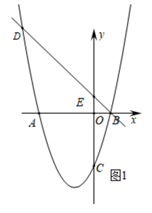 (1)、求抛物线 的解析式;(2)、如图2,点 为 轴上一动点,连接 ,当 时,求点 的坐标;
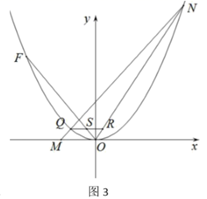
(1)、求抛物线 的解析式;(2)、如图2,点 为 轴上一动点,连接 ,当 时,求点 的坐标;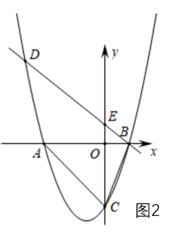 (3)、如图3,将抛物线 平移,使其顶点是坐标原点 ,得到抛物线 ;将直线 向下平移经过坐标原点 ,交抛物线 于另一点 .点 ,点 是 上且位于第一象限内一动点, 交 于 点, 轴分别交 于 ,试说明: 与 存在一个确定的数量关系.
(3)、如图3,将抛物线 平移,使其顶点是坐标原点 ,得到抛物线 ;将直线 向下平移经过坐标原点 ,交抛物线 于另一点 .点 ,点 是 上且位于第一象限内一动点, 交 于 点, 轴分别交 于 ,试说明: 与 存在一个确定的数量关系.