初中数学人教版七年级上学期第二章整式的加减

试卷更新日期：2020-08-03 类型：单元试卷

进入出卷网下载

一、单选题

1. 已知单项式 $\frac{1}{2} x y^{3}$ 与 $- 3 x y^{4 + a}$ 是同类项，那么a的值是（）

A、-1 B、0 C、1 D、2

查看试题解析
2. 关于单项式2³x²y²z，下列结论正确的是（）

A、系数是-2，次数是 4 B、系数是-2，次数是 5 C、系数是-2，次数是 8 D、系数是 2³ ，次数是 5

查看试题解析
3. 下列说法正确的是（）

A、单项式 $- a$ 的系数是 $1$ ； B、单项式 $- 3 a b c^{2}$ 的次数是 $3$ ； C、 $4 a^{2} b^{2} - 3 a^{2} b + 1$ 是四次多项式； D、 $m^{2} n^{5}$ 不是整式；

查看试题解析
4. 下列计算正确的是（）

A、 $5 a - 2 a = 3$ B、 $2 a + 3 b = 5 a b$ C、 $3 a + 2 a = 5 a^{2}$ D、 $- 3 a b + b a = - 2 a b$

查看试题解析
5. 下列去括号中，正确的是（）

A、 $- (a + b + c) = - a + b - c$ B、 $- 2 (a + b - 3 c) = - 2 a - 2 b + 6 c$ ． C、 $- (- a - b - c) = - a + b + c$ D、 $- (a - b - c) = - a + b - c$

查看试题解析
6. 任意给定一个非零数 $x$ ，按下列箭头顺序执行方框里的相应运算，得出结果后，再进行下一方框里的相应运算，最后得到的结果是（）
$x \to$ 平方 $\to + x \to \div x \to - 2 \to$ 结果

A、 $x$ B、 $x^{2}$ C、 $x + 1$ D、 $x - 1$

查看试题解析
7. 一组按规律排列的多项式：ab，a²b³ ， a³b⁵ ， a⁴b⁷ ， ⋯⋯，其中第 10 个式子是（）

A、a¹⁰ b¹⁵ B、a¹⁰ b¹⁹ C、a¹⁰ b¹⁷ D、a¹⁰ b²¹

查看试题解析
8. 如图，桌上有9张卡片，每张卡片的一面写数字1，另一面写数字-1.每次翻动任意2张(包括已翻过的牌)。改变其向上的面，然后计算能看到的所有牌面数字的积请问，当翻了2019次时牌面数字的积为（）

A、1 B、-1 C、2019 D、-2019

查看试题解析
9. 如图是一组有规律的图案，它们是由边长相同的小正方形组成，其中部分小正方形涂有阴影，依此规律，第10个图案中涂有阴影的小正方形的个数为（）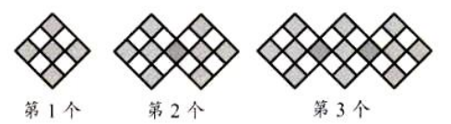

A、50 B、45 C、41 D、36

查看试题解析
10. 一个长方形的宽是 $a$ ，长是 $2 a$ ，则这个长方形的周长是（）

A、 $3 a$ B、 $6 a$ C、 $2 a^{2}$ D、 $9 a$

查看试题解析

二、填空题

11. 计算： $- a - 3 a =$ .

查看试题解析
12. 多项式 2x²y-xy的次数是．

查看试题解析
13. 写出一个3次单项式。

查看试题解析
14. 把多项式 $3 a^{2} b^{2} - a^{3} b - 1 - a b^{3}$ 按字母 $a$ 升幂排列后，第二项是.

查看试题解析
15. 关于m、n的单项式 $2 m^{a} n^{b} 与 - 3 m^{2 (a - 1)} n$ 的和仍为单项式，则这个和为

查看试题解析
16. 如图所示的运算程序中，若开始输入的 $x$ 值为12，我们发现第1次输出的结果为6，第2次输出的结果为3，…，第2020次输出的结果为.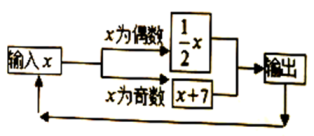

查看试题解析
17. 多项式 $x^{2} - 3 m x y - 3 y^{2} + 6 x y - 8$ 中不含 $x y$ 项，则常数 $m$ 的值是.

查看试题解析
18. 如图，下列各三角形中的三个数之间均具有相同的规律，根据此规律，最后一个三角形中y与n之间的关系是(n≥1)。

查看试题解析
19. 一组按规律排列的式子： $- \frac{9}{2} ， \frac{16}{6} ， - \frac{25}{12} ， \frac{36}{20}$ …照此规律第9个数为

查看试题解析

三、计算题

20. 化简求值：3x³-(4x²+5x)-3(x³-2x²-2x)，其中x=-2。

查看试题解析
21. 先化简，再求值： $3 a^{2} b - [- 2 a^{2} b - 6 (a b - \frac{2}{3} a^{2} b) + 4 a b] - 3 a b$ ，其中 $a = 3$ ， $b = - \frac{1}{3}$ ．

查看试题解析
22. 已知2x^my²与－3xyⁿ是同类项，试计算下面代数式的值：m－(m²n＋3m－4n)＋(2nm²－3n)．

查看试题解析
23. 若关于x，y的多项式my³＋3nx²y＋2y³－x²y＋y不含三次项，求2m＋3n的值．

查看试题解析

四、解答题

24. 有这样一道题：“计算(2x³－3x²y－2xy²)－(x³－2xy²＋y³)＋(－x³＋3x²y－y³)的值，其中x＝ $\frac{1}{2}$ ，y＝－1.”甲同学把“x＝ $\frac{1}{2}$ ”错抄成“x＝－ $\frac{1}{2}$ ”，但他计算的结果也是正确的，试说明理由，并求出正确结果．

查看试题解析
25. 已知A=2x²+3xy﹣2x﹣1，B=x²﹣xy﹣1.

(1)、化简：4A﹣（2B+3A），将结果用含有x、y的式子表示；

(2)、若式子4A﹣（2B+3A）的值与字母x的取值无关，求y³+ $\frac{7}{125}$ A﹣ $\frac{14}{125}$ B的值.

查看试题解析
26. 观察下列等式： $\frac{1}{1 \times 2}$ =1﹣ $\frac{1}{2}$ ， $\frac{1}{2 \times 3}$ = $\frac{1}{2}$ ﹣ $\frac{1}{3}$ ， $\frac{1}{3 \times 4}$ = $\frac{1}{3}$ ﹣ $\frac{1}{4}$ ，…．
将以上三个等式两边分别相加得： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ =1﹣ $\frac{1}{2}$ + $\frac{1}{2}$ ﹣ $\frac{1}{3}$ + $\frac{1}{3}$ ﹣ $\frac{1}{4}$ =1﹣ $\frac{1}{4}$ = $\frac{3}{4}$ ．

(1)、猜想并写出： $\frac{1}{n (n + 1)}$ = ．

(2)、直接写出下列各式的计算结果：
① $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…+ $\frac{1}{2016 \times 2017}$ =；

② $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ +…+ $\frac{1}{n (n + 1)}$ = ．

(3)、探究并计算： $\frac{1}{2 \times 4}$ + $\frac{1}{4 \times 6}$ + $\frac{1}{6 \times 8}$ +…+ $\frac{1}{2014 \times 2016}$ ．

查看试题解析

初中数学人教版七年级上学期 第二章 整式的加减

一、单选题

二、填空题

三、计算题

四、解答题

初中数学人教版七年级上学期第二章整式的加减