初中数学人教版八年级上册 第十四章 14.2乘法公式
试卷更新日期:2020-08-02 类型:同步测试
一、单选题
-
1. 下列多项式乘法中可以用平方差公式计算的是( )A、(﹣a+b)(a﹣b) B、(x+2)(2+x) C、( +y)(y﹣ ) D、(x﹣2)(x+1)2. 计算: =( )A、 B、 C、 D、3. 计算(x﹣y+z)(x+y﹣z)的正确结果为( )A、x2﹣y2+2xy﹣z2 B、x2﹣2xy+y2﹣z2 C、x2+2xy+y2﹣z2 D、x2+y2﹣2xy+z24. 下列式子正确的是( )A、
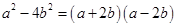 B、
B、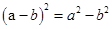 C、
C、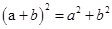 D、
D、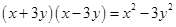 5. 若x2﹣xy+2=0,y2﹣xy﹣4=0,则x﹣y的值是( )A、﹣2 B、2 C、±2 D、±6. 若x2+kx+81是一个完全平方式,则k的值为( )A、18 B、﹣18 C、±9 D、±187. 如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是( )
5. 若x2﹣xy+2=0,y2﹣xy﹣4=0,则x﹣y的值是( )A、﹣2 B、2 C、±2 D、±6. 若x2+kx+81是一个完全平方式,则k的值为( )A、18 B、﹣18 C、±9 D、±187. 如图,边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后,剩余部分又剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是( )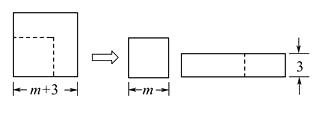 A、2m+3 B、2m+6 C、m+3 D、m+68. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( )
A、2m+3 B、2m+6 C、m+3 D、m+68. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由三角形较长直角边长为a,较短直角边长为b,若(a+b)2=21,大正方形的面积为13,则小正方形的面积为( ) A、3 B、4 C、5 D、69. 下列各数能整除 212-1的是( )A、11 B、13 C、63 D、6410. 如图,从边长为a的正方形中去掉一个边长为b的小正方形,然后将剩余部分剪后拼成一个长方形,上述操作能验证的等式是( )
A、3 B、4 C、5 D、69. 下列各数能整除 212-1的是( )A、11 B、13 C、63 D、6410. 如图,从边长为a的正方形中去掉一个边长为b的小正方形,然后将剩余部分剪后拼成一个长方形,上述操作能验证的等式是( )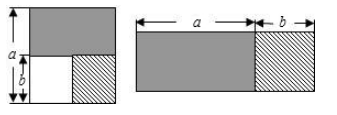 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 某多项式可以因式分解为a(a+2b)(-2b+a),则该多项式为。13. 若 , , ,则代数式 的值为.14. 已知x2+=2,则+x9++x= .
三、计算题
-
15. 已知a-b=7,ab=-10.求:(1)、a2+b2的值;(2)、(a+b)2+2(a-b)2的值.16. 用简便方法计算:(1)、1002-200×99+992(2)、2018×2020-20192
四、解答题
-
17. 试说明不论x,y取何值,代数式x2+y2+6x-4y+15的值总是正数.18. 已知:a,b,c为△ABC的三边长,且2a2+2b2+2c2=2ab+2ac+2bc,试判断△ABC的形状,并证明你的结论。19. 阅读并完成下列各题:
通过学习,同学们已经体会到灵活运用整式乘法公式给计算和化简带来的方便、快捷.相信通过下面材料的学习、探究,会使你大开眼界,并获得成功的喜悦.
【例】用简便方法计算995×1005.
解:995×1005
=(1000﹣5)(1000+5)①
=10002﹣52②
=999975.
(1)、例题求解过程中,第②步变形是利用(填乘法公式的名称);(2)、用简便方法计算:①9×11×101×10 001;
②(2+1)(22+1)(24+1)…(232+1)+1.