初中数学人教版八年级上册 第十三章 13.3等腰三角形
试卷更新日期：2020-08-02 类型：同步测试
一、单选题
-
1. 如果等腰三角形有一个内角为 ，则其底角的度数是（ ）A、 B、 C、 或 D、不确定2. 已知等腰三角形的底边长为4，腰长为9，则它的周长为（ ）A、13 B、17 C、22 D、17或223. △ABC中，AB=AC，∠A=∠C，则△ABC是（ ）A、等腰三角形 B、等边三角形 C、不等边三角形 D、不能确定4. 在△ABC中，∠A：∠B：∠C＝2：2：5，则△ABC是（ ）A、等腰三角形 B、等边三角形 C、直角三角形 D、锐角三角形5. 如图， ， ， ，若 ，则 （ ）
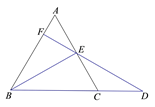A、 B、 C、 D、6. 如图在3×3的网格中，点A、B在格点处：以AB为一边，点P在格点处，则使△ABP为等腰三角形的点P有（ ）个
A、2个 B、3个 C、4个 D、5个7. 有下列命题：①等腰三角形的角平分线、中线和高重合；②等腰三角形两腰上的高相等；③有个外角等于120°的等腰三角形是等边三角形；④等边三角形的高线、中线、角平分线都相等；其中正确的有（ ）A、1个 B、2个 C、3个 D、4个8. 已知等腰三角形△ABC，BC边上的高恰好等于BC边长的一半，则∠BAC的度数是（ ）A、75° B、90°或75° C、90°或 75°或15° D、75°或15°或60°二、填空题
-
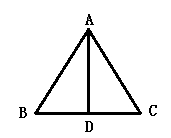
9. 如图，在△ABC中，AB=AC，BC=10，AD是∠BAC平分线，则BD=.
10. 已知等腰三角形的其中两边长为6cm和8cm，则这个三角形的周长为cm.11. 如图，△ABC中，AB=AC，∠BAC=120°，DE⊥AC，交AC于点D，交BC于点E，F是CE上一点，ED=EF，连接DF，DE=2cm，则CE的长为cm。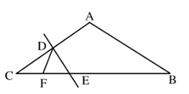
12. 若等腰三角形的顶角为α，则一腰上的高线与另一腰的夹角是(用α的代数式表示)
13. 如图，△ABC中，∠B、∠C的平分线交于点O，过O点作EF∥BC交AB、AC于E、F，EF=5，BE=2，则CF=.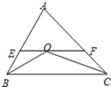
14. 在△ABC中，∠C=90°，AC=8cm．BC=6 cm， 动点P从点C开始，按C→A→B→C的路径绕△ABC的边运动一周，速度为每秒2cm，运动的时间为t秒．则△BCP为等腰三角形时t的值是 ．三、解答题
-
15. 已知：如图， ， ，求证： 是等腰三角形.
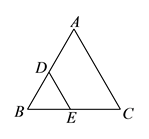16. 如图，已知△ABC中，点D、E在BC上，AB=AC，AD=AE。请说明BD=CE的理由。
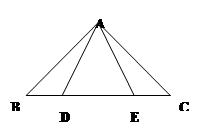17. 如图，在△ABC中，已知AB＝AC，∠BAC和∠ACB的平分线相交于点D，∠ADC＝125°.求∠ACB和∠BAC的度数.
18. 如图，在△ABC中，∠BAC=90°，AD⊥BC，BE平分∠ABC，G为EF的中点，求证：AG⊥EF
19. 如图，已知在△ABC中，△ABC的外角∠ABD的平分线与∠ACB的平分线交于点O，MN过点O，且MN∥BC，分别交AB、AC于点M、N．求证：MN=CN﹣BM．
20.如图，已知在△ABC中，AB=AC=10cm，BC=8cm，D为AB中点，设点P在线段BC上以3cm/秒的速度由B点向C点运动，点Q在线段CA上由C点向A点运动.
(1)、若Q点运动的速度与P点相同，且点P，Q同时出发，经过1秒钟后△BPD与△CQP是否全等，并说明理由；(2)、若点P，Q同时出发，但运动的速度不相同，当Q点的运动速度为多少时，能在运动过程中有△BPD与△CQP全等？(3)、若点Q以（2）中的速度从点C出发，点P以原来的速度从点B同时出发，都是逆时针沿△ABC的三边上运动，经过多少时间点P与点Q第一次在△ABC的哪条边上相遇？