2021高考一轮复习 第九讲 对数与对数函数
试卷更新日期:2020-08-02 类型:一轮复习
一、单选题
-
1. 已知55<84 , 134<85 . 设a=log53,b=log85,c=log138,则( )A、a<b<c B、b<a<c C、b<c<a D、c<a<b2. 设 ,则 ( )A、 B、 C、 D、3. 函数f(x)=loga(4-x)(a>0,且a≠1)的定义域是( )A、(0,4) B、(4,+∞) C、(-∞,4) D、(-∞,4)∪(4,+∞)4. 设 均为正数且 ,则 的最大值为( )A、1 B、2 C、10 D、205. 已知正项等比数列{an},若向量 , , ,则 =( )A、12 B、 C、5 D、186. 函数 的大致图象是( )A、
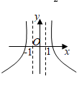 B、
B、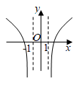 C、
C、 D、
D、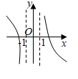 7. 已知幂函数 的图象过点 ,则 的值为( )A、 B、 C、2 D、8. 命题p:存在实数 ,对任意实数x,使得 恒成立; : , 为奇函数,则下列命题是真命题的是( )A、 B、 C、 D、9. 已知函数 若方程f(x)=m有4个不同的实根x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则( )(x3+x4)=( )A、6 B、7 C、8 D、910. 已知函数 ,若 ,则 ( )A、 B、 C、 D、
7. 已知幂函数 的图象过点 ,则 的值为( )A、 B、 C、2 D、8. 命题p:存在实数 ,对任意实数x,使得 恒成立; : , 为奇函数,则下列命题是真命题的是( )A、 B、 C、 D、9. 已知函数 若方程f(x)=m有4个不同的实根x1 , x2 , x3 , x4 , 且x1<x2<x3<x4 , 则( )(x3+x4)=( )A、6 B、7 C、8 D、910. 已知函数 ,若 ,则 ( )A、 B、 C、 D、二、填空题
-
11. 数列 满足 ,且x1+x2+……+x100=100,则lg(x101+x102+……+x200)= .12. 函数 的定义域为 .13. 计算 的值为.14. 已知函数 ( 且 )的图象恒过定点P,且点P在函数 的图象上,则 .15. 若 ,则 的最小值为.16. 已知函数 ,则 的值为17. 关于函数 有下列四个命题:
①函数 在 上是增函数;
②函数 的图象关于 中心对称;
③不存在斜率小于 且与函数 的图象相切的直线;
④函数 的导函数 不存在极小值.
其中正确的命题有.(写出所有正确命题的序号)
三、解答题