初中数学浙教版八年级上册第3章 一元一次不等式 单元检测(提高篇)
试卷更新日期:2020-08-02 类型:单元试卷
一、单选题
-
1. 下列说法不一定成立的是( )A、若a>b,则a+c>b+c B、若a+c>b+c,则a>b C、若a>b,则ac2>bc2 D、若ac2>bc2 , 则a>b2. 用三个不等式a>b,ab>0, > 中的两个不等式作为题设,余下的一个不等式作为结论组成一个命题组成真命题的个数为( )A、0 B、1 C、2 D、33. 下列命题中,假命题的个数是( )
①一元一次不等式的解集可以只含一个解②一元一次不等式组的解集可以只含一个解③一元一次不等式组的解集可以不含任何一个解④x=2是不等式x+3≥5的解集
A、0个 B、1个 C、2个 D、3个4. 设a , b , c , d都是整数,且a<2b , b<3c , c<4d , d<20,则a的最大值是( )A、480 B、479 C、448 D、4475. 某商品的标价比成本价高m%,根据市场需要,该商品需降价n%出售,为了不亏本,n应满足( )
A、n≤m B、n≤ C、n≤ D、n≤6. 关于 的不等式 ,下列说法正确的是( )A、解集为 B、解集为 C、解集为 取任何实数 D、无论 取何值,不等式肯定有解7. △ABC的两条高的长度分别为4和12,若第三条高也为整数,则第三条高的长度是( )
A、4 B、4或5 C、5或6 D、68. 运行程序如图所示,从“输入实数 x”到“结果是否<18”为一次程序操作,若输入 x 后程序操作仅进行了三次就停止,那么 x 的取值范围是( )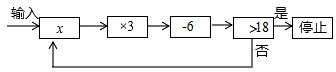 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 已知关于 x 的不等式 ax+b>0 的解集为 , 则不等式 bx+a<0 的解集是 .(结果中不含 a、b)10. 已知x=4是不等式ax-3a-1<0的解,x=2不是不等式ax-3a-1<0的解,则实数a的取值范围是.11. 参加学校科普知识竞赛决赛的5名同学A,B,C,D,E在赛后知道了自己的成绩,想尽快得知比赛的名次,大家互相打听后得到了以下消息:(分别以相应字母来对应他们本人的成绩)
信息序号
文字信息
数学表达式
1
C和D的得分之和是E得分的2倍
2
B的得分高于D
B>D
3
A和B的得分之和等于C和D的总分
4
D的得分高于E
请参照表中第二条文字信息的翻译方式,在表中写出其它三条文字信息的数学表达式,并根据上述信息猜一猜谁的得分最高:.
12. 下边的框图表示解不等式3-5x>4-2x 的流程,其中“系数化为 1”这一步骤的依据是 .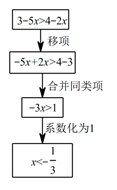 13. 有10名菜农,每人可种甲种蔬菜3亩乙种蔬菜2亩,已知甲种蔬菜每亩可收入0.5万元,乙种蔬菜每亩可收入0.8万元,若要使收入不低于15.6万元,则最多只能安排人种甲种蔬菜.14. 已知:不等式2x-m≤0只有三个正整数解,则化简 +|m-9|= .15. 邮政部门规定:信函重100克以内(包括100克)每20克贴邮票0.8元,不足20克重以20克计算;超过100克,先贴邮票4元,超过100克部分每100克加贴邮票2元,不足100克重以100克计算.八(9)班有11位同学参加项目化学习知识竞赛,若每份答卷重12克,每个信封重4克,将这11份答卷分装在两个信封中寄出,所贴邮票的总金额最少是元.16. 如图,三角形 中,A,B,C三点的坐标分别为 , , ,点 是 轴上一动点,若 ,则m的取值范围是.
13. 有10名菜农,每人可种甲种蔬菜3亩乙种蔬菜2亩,已知甲种蔬菜每亩可收入0.5万元,乙种蔬菜每亩可收入0.8万元,若要使收入不低于15.6万元,则最多只能安排人种甲种蔬菜.14. 已知:不等式2x-m≤0只有三个正整数解,则化简 +|m-9|= .15. 邮政部门规定:信函重100克以内(包括100克)每20克贴邮票0.8元,不足20克重以20克计算;超过100克,先贴邮票4元,超过100克部分每100克加贴邮票2元,不足100克重以100克计算.八(9)班有11位同学参加项目化学习知识竞赛,若每份答卷重12克,每个信封重4克,将这11份答卷分装在两个信封中寄出,所贴邮票的总金额最少是元.16. 如图,三角形 中,A,B,C三点的坐标分别为 , , ,点 是 轴上一动点,若 ,则m的取值范围是.
三、计算题
-
17. 解下列不等式
(1)、2(x-1)-3x>4(x+1)+5(2)、(3)、(4)、(5)、(6)、18. 若2a+b=12,其中a≥0,b≥0,又P=3a+2b.试确定P的最小值和最大值.19. 已知a1 , a2 , a3 , a4 , a5 , a6 , a7是彼此互不相等的正整数,它们的和等于159,求其中最小数a1的最大值.20. 如图,某景区内的环形路是边长为1200米的正方形ABCD,现有1号、2号两辆游览车分别从出口A和景点C同时出发,1号车沿A→B→C→D→A路线、2号车沿C→B→A→D→C路线连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为300米/分.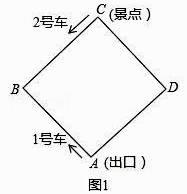
 (1)、如图1,设行驶时间为t分(0≤t≤8)
(1)、如图1,设行驶时间为t分(0≤t≤8)①1号车、2号车离出口A的路程分别为 ▲ 米, ▲ 米;(用含t的代数式表示)
②当两车相距的路程是600米时,求t的值;
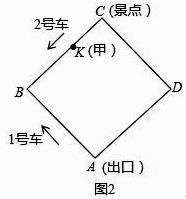
(2)、如图2,游客甲在BC上的一点K(不与点B、C重合)处候车,准备乘车到出口A,设CK=x米.情况一:若他刚好错过2号车,则他等候并搭乘即将到来的1号车;
情况二:若他刚好错过1号车,则他等候并搭乘即将到来的2号车.
请判断游客甲在哪种情况下乘车到出口A用时较多?(含候车时间)
21. 对x,y定义一种新运算T,规定 (其中a,b均为非零常数),这里等式右边是通常的四则运算,例: .已知 , .
(1)、求a,b的值;(2)、若关于m的不等式组 恰好有3个整数解,求实数p的取值范围.22. 随着出行方式的多样化,我市三类打车方式的收费标准如下:出租车
滴滴快车
同城快车
3千米以内:8元
路程:1.4元/千米
路程:1.8元/千米
超过3千米的部分:2.4元/千米
时间:0.6元/分钟
时间:0.4元/分钟
如:假设打车的平均车速为40千米/小时,乘坐8千米,耗时8÷40×60=12分钟,出租车的收费为:8+2.4×(8﹣3)=20(元);滴滴快车的收费为:8×1.4+12×0.6=18.4(元);同城快车的收费为:8×1.8+12×0.4=19.2(元)
解决问题:
(1)、小明乘车从高邮文体公园去盂城驿,全程10千米,如果小明使用滴滴快车,需要支付的打车费用为元;(2)、小丽乘车从甲地去乙地,用滴滴快车比乘坐出租车节省了28.8元,求甲、乙两地的距离;(3)、同城快车为了和滴滴快车竞争客户,分别推出了优惠方式:滴滴快车对于乘车路程在5千米以上(含5千米)的客户每次收费立减11元;同城快车车费对折优惠.通过计算,对同城快车和滴滴快车两种打车方式,采用哪一种打车方式更合算提出你的建议.