初中数学浙教版八年级上册3.4 一元一次不等式组 同步练习
试卷更新日期:2020-08-02 类型:同步测试
一、单选题
-
1. 下列不等式组是一元一次不等式组的是( )A、 B、 C、 D、2. 不等式组 的解集为( )A、x<1 B、x>2 C、x<1或 x>2 D、无解3. 下列不等式求解的结果,正确的是( )A、不等式组 的解集是 B、不等式组 的解集是 C、不等式组 无解 D、不等式组 的解集是4. 利用数轴确定不等式组 的解集,正确的是( )A、
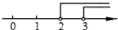 B、
B、 C、
C、 D、
D、 5. 不等式组 的解集在数轴上表示正确的是( )A、
5. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、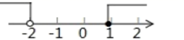 D、
D、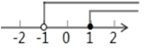 6. 若关于x的不等式组 有解,则m的取值范围是( )A、m<5 B、m>5 C、m≤5 D、m≥57. 不等式组 的整数解是( )A、15 B、16 C、17 D、15,18. 若不等式组 的整数解共有三个,则 的取值范围是( )A、 B、 C、 D、9. 已知关于x的不等式组 的解集中任意一个x的值均不在0≤x≤4的范围内,则a的取值范围是( )A、a>5或a<﹣2 B、﹣2≤a≤5 C、﹣2<a<5 D、a≥5或a≤﹣210. 今年四月份,李大叔收获洋葱30吨,黄瓜13吨.现计划租用甲、乙两种货车共10辆将这两种蔬菜全部运往外地销售,已知一辆甲种货车可装洋葱4吨和黄瓜1吨,一辆乙种货车可装洋葱和黄瓜各2吨.李大叔租用甲、乙两种货车时有( )种方案.A、1 B、2 C、3 D、4
6. 若关于x的不等式组 有解,则m的取值范围是( )A、m<5 B、m>5 C、m≤5 D、m≥57. 不等式组 的整数解是( )A、15 B、16 C、17 D、15,18. 若不等式组 的整数解共有三个,则 的取值范围是( )A、 B、 C、 D、9. 已知关于x的不等式组 的解集中任意一个x的值均不在0≤x≤4的范围内,则a的取值范围是( )A、a>5或a<﹣2 B、﹣2≤a≤5 C、﹣2<a<5 D、a≥5或a≤﹣210. 今年四月份,李大叔收获洋葱30吨,黄瓜13吨.现计划租用甲、乙两种货车共10辆将这两种蔬菜全部运往外地销售,已知一辆甲种货车可装洋葱4吨和黄瓜1吨,一辆乙种货车可装洋葱和黄瓜各2吨.李大叔租用甲、乙两种货车时有( )种方案.A、1 B、2 C、3 D、4二、填空题
-
11. 不等式组 的最小整数解为.12. 若不等式组 的解集为x<2m-2,则m的取值范围是 。13. 关于 的不等式组 的整数解仅有2,3,4,则 的取值范围是 , 的取值范围是 .14. 已知不等式组 无解,则 的取值范围是 .15. 某校今年冬季烧煤取暖时间为4个月,如果每月比计划多烧5吨煤,那么取暖用煤总量将超过100吨;如果每月比计划少烧5吨,那么取暖用煤总量不足68吨,该校计划每月烧煤多少吨?设该校计划每月烧煤 吨,根据题意可列不等式组。
三、计算题
-
16. 解关于x的不等式组 ,并把解集表示在数轴上。17. 解不等式组 ,并求它的整数解.18. 某班有住校生若干人,若每个房间住4人,则剩下20人没有宿舍住;若每个房间住8人,则有一间宿舍住不满.求有多少间宿舍,多少名学生?
