初中数学浙教版八年级上册3.2 不等式的基本性质同步练习

试卷更新日期：2020-08-02 类型：同步测试

进入出卷网下载

1. 若m＞n，则下列不等式正确的是（）

A、m－4＜n－4 B、 $\frac{m}{4} > \frac{n}{4}$ C、 4m＜4n D、－2m＞－2n

查看试题解析
2. 下列不等式总成立的是（　　）

A、4a＞2a B、a²＞0 C、a²＞a D、- $\frac{1}{2}$ ²≤0

查看试题解析
3. 下列不等式变形中正确的是（）

A、若a<b ，则a-b<b-1 B、若a>b ，则ac²>bc² C、若a-3>-3，则a>0 D、若ab>0，则a<0，b<0

查看试题解析
4. 有一道这样的题：“由★x>1得到x< $\frac{1}{★}$ ”，则题中★表示的是（）

A、非正数 B、正数 C、非负数 D、负数

查看试题解析
5. 实数a，b，c在数轴上对应的点如图所示，则下列式子一定成立的是（）

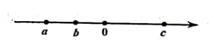A、a-c>b-c B、ac>bc C、a+c<b+c D、 $\frac{a}{b} < \frac{c}{b}$

查看试题解析
6. 下列判断正确的是（）

A、若 $7 a < - 7 b$ ，则 $a > - b$ B、若 $- 2 x < 3$ ，则 $x > - \frac{2}{3}$ C、若 $3 - a < 3 - b$ ，则 $a > b$ D、若 $a > b$ ， $c < d$ ，则 $a + c > b + d$

查看试题解析
7. 若 $a > b > 0$ ，则下列不等式不一定成立的是（）

A、 $a - 2 > b - 2$ B、 $- 2 a < - 2 b$ C、 $\sqrt{a} > \sqrt{b}$ D、 $m a > m b$

查看试题解析
8. 关于式子a+1的值，下列说法正确的是（）

A、比1大 B、比100小 C、比a大 D、比2a小

查看试题解析

9. 若 $m < n$ ，则2-3m2-3n(填“ $>$ ”或“ $<$ ”)．

查看试题解析
10. 根据不等式的基本性质，可将“mx＜2”化为“x＞ $\frac{2}{m}$ ”，则m的取值范围是.

查看试题解析
11. 如果a＞b ，则－ac²－bc²(c≠0)．

查看试题解析
12. 若a＞b，且 $\frac{a}{b} < 1$ ，则b0．（填“＞”或“＜”）

查看试题解析
13. 小明说不等式 $a > 2 a$ 永远不会成立，因为如果在这个不等式两边同时除以 $a$ ，就会出现 $1 > 2$ 这样的不符合题意结论.小明的说法（填写符合题意或不符合题意）；如果符合题意请说明理由,不符合题意请举一个反例说明：．

查看试题解析

初中数学浙教版八年级上册3.2 不等式的基本性质 同步练习