初中数学人教版七年级上学期第三章 3.3解一元一次方程（二）去括号与去分母

试卷更新日期：2020-08-01 类型：同步测试

进入出卷网下载

一、单选题

1. 下列解方程中去分母正确的是（）

A、由 $\frac{x}{3} - 1 = \frac{1 - x}{2}$ ，得 $2 x - 1 = 3 - 3 x$ B、由 $\frac{x - 2}{2} - \frac{3 x - 2}{4} = - 1$ ，得 $2 (x - 2) - 3 x - 2 = - 4$ C、由 $\frac{y + 1}{2} = \frac{y}{3} - \frac{3 y - 1}{6} - y$ ，得 $3 y + 3 = 2 y - 3 y + 1 - 6 y$ D、由 $\frac{4 y}{5} - 1 = \frac{y + 4}{3}$ ，得 $12 y - 1 = 5 y + 20$

查看试题解析
2. 解方程 $2 (3 x - 1) - (x - 4) = 1$ 时，去括号正确的是（）

A、 $6 x - 1 - x - 4 = 1$ B、 $6 x - 1 - x + 4 = 1$ C、 $6 x - 2 - x - 4 = 1$ D、 $6 x - 2 - x + 4 = 1$

查看试题解析
3. 方程 $\frac{x + 1}{2} - \frac{k x + 1}{3} = 1$ 的解为x=－5，则k为（）

A、2 B、1 C、0 D、－1

查看试题解析
4. 对于非零的两个实数a、b，规定a⊗b=2b﹣a ，若1⊗（x+1）=1，则x的值为）

A、 $- 1$ B、1 C、 $\frac{1}{2}$ D、0

查看试题解析
5. 有一道解方程的题: $3 x - (5 □ x) = - 7 ，$ “□”处在印刷时被油墨盖住了,查阅后面的答案得知这个方程的解是 $x = - 2$ 那么“□”处应该是（）

A、 $- 2$ B、 $+ 2$ C、 $+ 3$ D、 $- 3$

查看试题解析
6. 下列解方程过程中，变形正确的是(　　)

A、由5x﹣1＝3，得5x＝3﹣1 B、由 $\frac{x}{4}$ +1＝ $\frac{3 x + 1}{0.1}$ +12，得 $\frac{x}{4}$ +1＝ $\frac{3 x + 10}{1}$ +12 C、由3﹣ $\frac{x - 1}{2}$ ＝0，得6﹣x+1＝0 D、由 $\frac{x}{3} - \frac{x}{2}$ ＝1，得2x﹣3x＝1

查看试题解析
7. 在有理数范围内定义运算“*”，其规则为a*b＝ $- \frac{2 a + b}{3}$ ，则方程（2*3）（4*x）＝49的解为（　　）

A、﹣3 B、﹣55 C、﹣56 D、55

查看试题解析

二、填空题

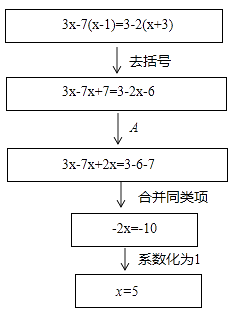
8. 在公式 $s = \frac{1}{2} (a + b) h$ 中， $S = 120, b = 12, h = 8$ ，则a=

查看试题解析
9. 当a＝时，关于x的方程 $\frac{x + 2}{3} - \frac{3 x + a}{6} =1$ 的解是x＝－1.

查看试题解析
10. 方程 $\frac{x}{12} - \frac{5 x + 1}{6} - 1 = \frac{3 x - 2}{4}$ 去分母时，方程的两边应同时乘以，则得到的方程是.

查看试题解析
11. 解方程 $\frac{3 x + 1}{2} = 2 - \frac{2 x - 1}{6}$ ，有下列步骤：① $3 (3 x + 1) = 12 - (2 x - 1)$ ，② $9 x + 3 = 12 - 2 x + 1$ ，③ $9 x - 2 x = 12 + 1 + 3$ ，④ $7 x = 16$ ，⑤ $x = \frac{16}{7}$ ，其中首先发生错误的一步是．

查看试题解析
12. 当x=时，式子 $\frac{2 x + 5}{6}$ 与 $\frac{x + 11}{4} + x$ 的值互为相反数．

查看试题解析
13. 下面的框图表示解方程3x-7（x-1）=3-2（x+3）的流程，其中A代表的步骤是，步骤A对方程进行变形的依据是。

查看试题解析

三、计算题

14. 解方程： $5 (x - 8) - 5 = 0$ ．

查看试题解析
15. 解方程： $\frac{5 x - 7}{3} - 1 = 2 + \frac{x + 1}{2}$

查看试题解析
16. 解下列方程

(1)、 $3 - 2 (x - 1) = 1 - 2 (1 - \frac{1}{2} x)$

(2)、 $\frac{2 x + 1}{5} - 1 = \frac{2 x - 1}{4} - \frac{2 x + 1}{2}$

查看试题解析

四、解答题

17. 小李在解方程 $\frac{3 x + 5}{2} - \frac{2 x - m}{3} = 1$ 去分母时方程右边的1没有乘以6，因而得到方程的解为x=﹣4，求出m的值并符合题意解出方程．

查看试题解析
18. 下面是马小哈同学做的一道题，请按照“要求”帮他改正．
解方程： $\frac{3 x - 1}{2} = 1 + \frac{2 x + 3}{3}$

马小哈的解答

解： $3 (3 x - 1) = 1 + 2 (2 x + 3)$

$9 x - 3 = 1 + 4 x + 6$

$9 x - 4 x = 1 + 6 - 3$

$5 x = 4$

$x = \frac{4}{5}$

“要求”：

$①$ 用“-”画出解题过程中的所有不符合题意．

$②$ 请你把正确的解答过程写在下面．

查看试题解析
19. 依据下列解方程 $\frac{0.3 x + 0.5}{0.2} - 1 = \frac{2 x - 1}{3}$ 的过程，请在前面的括号内填写变形步骤，在后面的括号内填写变形依据．
解：原方程可变形为 $6 \times \frac{0.3 x + 0.5}{0.2} - 6 \times 1 = 6 \times \frac{2 x - 1}{3}$ （                          ）
去分母，得 $3 (3 x + 5) - 6 = 2 (2 x - 1)$ （                            ）
去括号，得 $9 x + 15 - 6 = 4 x - 2$ （                                ）
（          ），得 $9 x - 4 x = - 2 - 15 + 6$ （                              ）
合并同类项，得 $5 x = - 11$
系数化为1，得 $x = - \frac{11}{5}$ （                          ）

查看试题解析
20. 小明在解方程 $\frac{2 x - 1}{5} + 1 = \frac{x + a}{2}$ 时，方程左边的“+1”没有乘以10，因此求得方程的解为 $x = 4$ ，试求a的值及方程的正确解？

查看试题解析
21. 已知关于x的方程：2（x﹣1）+1＝x与3（x+m）＝m﹣1有相同的解，求以y为未知数的方程 $\frac{3 - m y}{3} = \frac{m - 3 x}{2}$ 的解．

查看试题解析

初中数学人教版七年级上学期 第三章 3.3解一元一次方程（二）去括号与去分母

一、单选题

二、填空题

三、计算题

四、解答题

初中数学人教版七年级上学期第三章 3.3解一元一次方程（二）去括号与去分母