初中数学苏科版八年级上册1.3 探索三角形全等的条件（适用于预习）

试卷更新日期：2020-08-01 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 下列说法正确的是（　　）
    A、形状相同的两个三角形全等 B、面积相等的两个三角形全等 C、完全重合的两个三角形全等 D、所有的等腰三角形都全等

    查看试题解析

  • 2. 如图，在△ABC和△DEF中，已有条件AB=DE，还需要添加两个条件才能使△ABC≌△DEF，不能添加的一组条件是（      ）

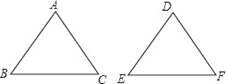    A、∠B=∠E，BC=EF B、∠A=∠D，BC=EF C、∠A=∠D，∠B=∠E D、BC=EF，AC=DF

    查看试题解析

  • 3.

    如图，已知∠1＝∠2，则不一定能使△ABD≌△ACD的条件是（  ）

    A、AB＝AC B、BD＝CD C、∠B＝∠C D、∠ BDA＝∠CDA

    查看试题解析

  • 4. 如图所示，点E，F分别在线段AB，AC上，CF与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACF（    ）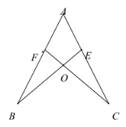

    A、∠B=∠C B、AE=AF C、BE=CF D、∠AEB=∠AFC

    查看试题解析

  • 5. 如图，将两根钢条 AA'，BB' 的中点连接在一起，使AA'，BB' 可以绕着点O自由转动，就做成了一个测量工具(卡钳)，则图中AB的长等于内槽宽 A′B′ ，那么判定 △OAB≌△OA′B′ 的理由是（ ）

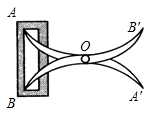    A、边角边 B、边边边 C、角边角 D、角角边

    查看试题解析

  • 6. 如图，△ABC的一角被墨水污了，但小明很快就画出跟原来一样的图形，他所用定理是（   ）

    A、SAS B、SSS C、ASA D、HL

    查看试题解析

  • 7. 如图，点E，F在BD上，AD=BC，DF=BE，添加下面四个条件中的一个，使△ADE≌△CBF的是（　　）

    ①∠A=∠C；②AE=CF；③∠D=∠B；④AE∥CF．

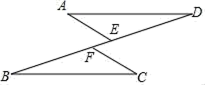    A、①或③ B、①或④ C、②或④ D、②或③

    查看试题解析

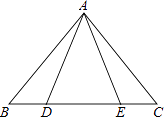
  • 8. 如图，等腰三角形ABC中，AB=AC，D、E都在BC上，要使△ABD≌△ACE，需要添加一个条件，某学习小组在讨论这个条件时给出了如下几种方案：

    ①AD=AE；②BD=CE；③BE=CD；④∠BAD=∠CAE，其中可行的有（   ）

    A、1种 B、2种 C、3种 D、4种

    查看试题解析

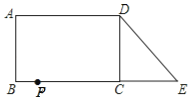
  • 9.

    已知：如图，在长方形ABCD中，AB=4，AD=6．延长BC到点E，使CE=2，连接DE，动点P从点B出发，以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动，设点P的运动时间为t秒，当t的值为（　　）秒时．△ABP和△DCE全等．


    A、1 B、1或3 C、1或7 D、3或7

    查看试题解析

  • 10.

    如图所示的4×4正方形网格中，∠1+∠2+∠3+∠4+∠5+∠6+∠7=（   ）

    A、330° B、315° C、310° D、320°

    查看试题解析

二、填空题

  • 11. 如图，已知点A、D、C、F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需添加一个条件是.

    查看试题解析

  • 12. 如图，所示某人将一块三角形的玻璃打碎成了四块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带去.

    查看试题解析

  • 13. 如图，已知△ABC中，AB=AC，AD平分∠BAC，请补充完整过程，说明△ABD≌△ACD的理由．

    查看试题解析

  • 14. 如图：有一个直角三角形ABC，∠C＝90°，AC＝10，BC＝5，一条线段PQ＝AB，P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动，问P点运动到离A的距离等于时，ΔABC和ΔPQA全等.

    查看试题解析

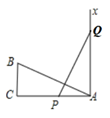  • 15. 如图，已知BC＝EC，∠BCE＝∠ACD，要使△ABC≌△DEC，则应添加的一个条件为 ． （答案不唯一，只需填一个）

    查看试题解析

  • 16. 如图，在Rt△ABC中，∠C=90°，AC=10，BC=5，PQ=AB，点P和点Q分别在AC和AC 垂线AD上移动，则当AP=时，才能使△ABC和△APQ全等.

    查看试题解析

三、综合题

  • 17. 已知：如图，AB∥CD，E是AB的中点，CE=DE．求证：

    (1)、∠AEC=∠BED；
    (2)、AC=BD．

    查看试题解析

  • 18. 如图：在△ABC中，BE、CF分别是AC、AB两边上的高，在BE上截取BD=AC，在CF的延长线上截取CG=AB，连接AD、AG．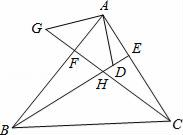

    (1)、求证：AD=AG；
    (2)、AD与AG的位置关系如何，请说明理由．

    查看试题解析

  • 19. 问题情境：如图①，在直角三角形ABC中，∠BAC= 900 ，AD⊥BC于点D，可知：∠BAD=∠C（不需要证明）；

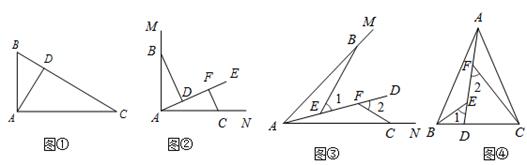    (1)、特例探究：如图②，∠MAN=90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB="AC，"CF⊥AE于点F，BD⊥AE于点

    D.证明：△ABD≌△CAF；

    (2)、归纳证明：如图③，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC，∠1=∠2=∠BA C．求证：△ABE≌△CAF；
    (3)、拓展应用：如图④，在△ABC中，AB=AC，AB＞B

    C.点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BA

    C.若△ABC的面积为15，则△ACF与△BDE的面积之和为.

    查看试题解析