初中数学浙教版七年级上册第3章 实数 单元检测（提高篇）
试卷更新日期：2020-08-01 类型：单元试卷
一、单选题
-
1. 若 ，则 的值不可能是（ ）A、 B、 C、 D、2. 若a为实数，下列各数中一定比a大的是（ ）A、|a| B、a+1 C、 D、﹣a3. 下列说法正确的是（ ）A、﹣81的平方根是±9 B、任何数的平方是非负数，因而任何数的平方根也是非负 C、任何一个非负数的平方根都不大于这个数 D、2是4的平方根4. 在数学课上，老师将一长方形纸片的长增加2 cm，宽增加7 cm，就成为了一个面积为192cm²的正方形，则原长方形纸片的面积为（ ）A、18cm² B、20cm² C、36cm² D、48cm²5. 一个立方体的体积是120m3 ， 它的棱长大约在（ ）A、4m与5m之间 B、5m与6m之间 C、6m与7m之间 D、7m与8m之间6. 下列四个式子：
① ；② ＜8；③ ＜1；④ ＞0.5．
其中大小关系正确的式子的个数是（ ）
A、1个 B、2个 C、3个 D、4个7. 实数a，b，c，d在数轴上的对应点的位置如图所示，则正确的结论是（ ）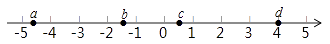
A、a>–4 B、bd>0 C、|a|>|d| D、b+c>08. 对于有理数 、 ，定义 的含义为：当 时， ，例如： .已知 ， ，且 和 为两个连续正整数，则 的立方根为（ ）A、 B、 C、 D、二、填空题
-
9. 若一正数的两个平方根分别是2a-1与-a+2，则a= ．10. 已知 ， ， ，则 等于 ．11. 试举一例，说明“两个无理数的和仍是无理数”是错误的：12. 观察被开方数a的小数点与算术平方根 的小数点的移动规律:
a
0.0001
0.01
1
100
10000
0.01
x
1
y
100
(1)、填空:x= ， y=.(2)、根据你发现的规律填空:①已知 ≈1.414，则 = ， =；
② = 0.274，记 的整数部分为x,则 =.
三、计算题
-
13. 计算：(1)、(2)、14.
(1)、已知 是最大的负整数， 是绝对值最小的数， 是倒数是它本身的正数， 是9的负平方根.① . . . .
②求
(2)、已知a与b互为相反数，c与d是倒数，求3（a+b）-（-cd）3-2的值.
15. 对于一个实数m（m≥0），规定其整数部分为a，小数部分为b，如：当m＝3时，则a＝3，b＝0；当m＝4.5时，则a＝4，b＝0.5.(1)、当m＝π时，b＝；当m＝ 时，a＝；(2)、当m＝9− 时，求a－b的值；(3)、若a－b＝ ，则m＝.16. 如图，用两个边长为15 cm的小正方形拼成一个大的正方形.
(1)、求大正方形的边长？(2)、若沿此大正方形边的方向剪出一个长方形，能否使剪出的长方形纸片的长宽之比为4：3且面积为720cm2.若能，试求出剪出的长方形纸片的长与宽；若不能，试说明理由？17. 如图，半径为1个单位的圆片上有一点A与数轴上的原点重合，AB是圆片的直径．(注：结果保留π)
(1)、把圆片沿数轴向右滚动半周，点B到达数轴上点C的位置，点C表示的数是数(填“无理”或“有理”)，这个数是；(2)、把圆片沿数轴滚动2周，点A到达数轴上点D的位置，点D表示的数是；(3)、圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动情况记录如下：+2，﹣1，+3，﹣4，﹣3．①第次滚动后，A点距离原点最近，第次滚动后，A点距离原点最远．
②当圆片结束运动时，A点运动的路程共有 ， 此时点A所表示的数是 ．
18. 我国数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题，求 的立方根.华罗庚脱口而出,你知道怎样迅速准确地计算出结果的吗？请按照下面的问题试一试：(1)、由 ,确定 的立方根是位数；(2)、由 的个位数是 确定 的立方根的个位数是；(3)、如果划去 后面的三位 得到数 ,而 ,由此能确定 的立方根的十位数是；所以 的立方根是；(4)、用类似的方法，请说出 的立方根是.