初中数学浙教版七年级上册第2章 有理数的运算 单元检测(提供篇)
试卷更新日期:2020-08-01 类型:单元试卷
一、单选题
-
1. 如图,乐乐将﹣3,﹣2,﹣1,0,1,2,3,4,5分别填入九个空格内,使每行、每列、每条对角线上的三个数之和相等,现在a、b、c分别标上其中的一个数,则a﹣b+c的值为( )
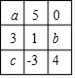 A、﹣1 B、0 C、1 D、32. 如果一个数的倒数等于它的本身,那么这个数一定是( )A、0 B、1 C、-1 D、±13. ,
A、﹣1 B、0 C、1 D、32. 如果一个数的倒数等于它的本身,那么这个数一定是( )A、0 B、1 C、-1 D、±13. ,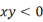 ,
, 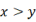 ,则有( ) A、
,则有( ) A、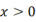 ,
, 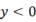 ,
,  绝对值较大
B、
绝对值较大
B、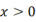 ,
, 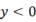 ,
, 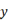 绝对值较大
C、 ,
绝对值较大
C、 , 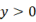 ,
,  绝对值较大
D、 ,
绝对值较大
D、 , 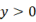 ,
, 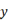 绝对值较大
4. 在算式(−0.3)□(1−0.3)中填上运算符号,使结果最大,这个运算符号是( )A、加号 B、减号 C、乘号 D、除号5. 2019 新型冠状病毒(2019-nCoV),因2019 年武汉病毒性肺炎病例而被发现,2020 年1月12日被世界卫生组织命名. 疫情发生以后, 国家发改委2 月7 日紧急下达第二批中央预算内投资2 亿元人民币,专项补助承担重症感染患者救治任务的湖北多家医院重症治疗病区建设,其中数据2 亿用科学记数法表示为 ( )A、2×107 B、2×108 C、20×107 D、0.2×1086. 中国奇书《易经》中记载,远古时期,人们通过在绳子上打结来计数,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满5进1,用来记录孩子自出生后的天数.由图可知,孩子自出生后的天数是( )
绝对值较大
4. 在算式(−0.3)□(1−0.3)中填上运算符号,使结果最大,这个运算符号是( )A、加号 B、减号 C、乘号 D、除号5. 2019 新型冠状病毒(2019-nCoV),因2019 年武汉病毒性肺炎病例而被发现,2020 年1月12日被世界卫生组织命名. 疫情发生以后, 国家发改委2 月7 日紧急下达第二批中央预算内投资2 亿元人民币,专项补助承担重症感染患者救治任务的湖北多家医院重症治疗病区建设,其中数据2 亿用科学记数法表示为 ( )A、2×107 B、2×108 C、20×107 D、0.2×1086. 中国奇书《易经》中记载,远古时期,人们通过在绳子上打结来计数,即“结绳计数”.如图,一位母亲在从右到左依次排列的绳子上打结,满5进1,用来记录孩子自出生后的天数.由图可知,孩子自出生后的天数是( )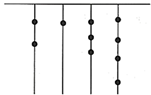 A、10 B、89 C、165 D、2947. 下列叙述正确的是( )A、近似数8.96×104精确到百分位 B、近似数5.3万精确到千位 C、0.130精确到百分位 D、若两个有理数的差大于0,则这两个有理数都大于08. 计算:1+( 2)+3+( 4)+…+2017+( 2018)的结果是( )A、0 B、 1 C、 1009 D、10109. 2017减去它的 ,再减去余下的 ,再减去余下的 ,…依次类推,一直减到余下的 ,则最后剩下的数是( )A、 B、 C、 D、10. 在1、2、3、…99、100这100个数中,任意加上“+”或“-”,相加后的结果一定是( )A、奇数 B、偶数 C、0 D、不确定
A、10 B、89 C、165 D、2947. 下列叙述正确的是( )A、近似数8.96×104精确到百分位 B、近似数5.3万精确到千位 C、0.130精确到百分位 D、若两个有理数的差大于0,则这两个有理数都大于08. 计算:1+( 2)+3+( 4)+…+2017+( 2018)的结果是( )A、0 B、 1 C、 1009 D、10109. 2017减去它的 ,再减去余下的 ,再减去余下的 ,…依次类推,一直减到余下的 ,则最后剩下的数是( )A、 B、 C、 D、10. 在1、2、3、…99、100这100个数中,任意加上“+”或“-”,相加后的结果一定是( )A、奇数 B、偶数 C、0 D、不确定二、填空题
-
11. 已知数 的大小关系如图所示:则下列各式:① ;② (-a) -b+c>0;③ ;④ ;⑤ .其中正确的有(请填写编号).
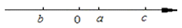 12. 三味书屋推出售书优惠方案:(1)一次性购书不超过100元,不享受优惠;(2)一次性购书超过100元但不超过200元一律打九折;(3)一次性购书超过200元及以上一律打八折。如果王明同学一次性购书162元,那么王明所购书的原价一定为.13. 将一根长1米的木棒,第一次截去一半,第二次截去剩下部分的一半,如此截下去,截至第五次,剩下的木棒长是米.14. 小志自主创业,在网上经营一家水果店,销售的水果中有盒装草莓、荔枝、山竹,价格依次为40元/盒、60元/盒、80元/盒.为增加销量,小志对这三种水果进行促销:一次性购买水果的总价超过100元时,超过的部分打5折,每笔订单限购3盒.顾客支付成功后,小志会得到支付款的80%作为货款.(1)、顾客一笔订单购买了上述三种水果各一盒,则小志收到的货款是元;(2)、小志在两笔订单中共售出原价180元的水果,则他收到的货款最少是元.15. 绝对值小于2019的所有整数之和为.16. 10位裁判给一位运动员打分,每个人给的分数都是整数,去掉一个最高分,再去掉一个最低分,其余得分的平均数为该运动员的得分。若用四舍五入取近似值的方法精确到十分位,该运动员得9.4分,如果精确到百分位,该运动员得分应当是分.
12. 三味书屋推出售书优惠方案:(1)一次性购书不超过100元,不享受优惠;(2)一次性购书超过100元但不超过200元一律打九折;(3)一次性购书超过200元及以上一律打八折。如果王明同学一次性购书162元,那么王明所购书的原价一定为.13. 将一根长1米的木棒,第一次截去一半,第二次截去剩下部分的一半,如此截下去,截至第五次,剩下的木棒长是米.14. 小志自主创业,在网上经营一家水果店,销售的水果中有盒装草莓、荔枝、山竹,价格依次为40元/盒、60元/盒、80元/盒.为增加销量,小志对这三种水果进行促销:一次性购买水果的总价超过100元时,超过的部分打5折,每笔订单限购3盒.顾客支付成功后,小志会得到支付款的80%作为货款.(1)、顾客一笔订单购买了上述三种水果各一盒,则小志收到的货款是元;(2)、小志在两笔订单中共售出原价180元的水果,则他收到的货款最少是元.15. 绝对值小于2019的所有整数之和为.16. 10位裁判给一位运动员打分,每个人给的分数都是整数,去掉一个最高分,再去掉一个最低分,其余得分的平均数为该运动员的得分。若用四舍五入取近似值的方法精确到十分位,该运动员得9.4分,如果精确到百分位,该运动员得分应当是分.三、解答题
-
17. 用简便方法计算:(1)、(2)、18. 小明编制了一个计算机计算程序,当输入任何一个有理数时,显示屏上的结果总等于所输入的这个数的绝对值与-2的和.若输入-3,这时显示的结果应当是多少?如果输入某数后,显示的结果是7,那么输入的数是多少?19. 阅读下面材料并完成填空,你能比较两个数20072008和20082007的大小吗?为了解决这个问题,先把问题一般化,即比较nn+1和(n+1)n的大小(n≥1的整数),然后,从分析这些简单情形入手,从中发现规律,经过归纳,猜想出结论.(1)、通过计算,比较下列各组两个数的大小(在横线上填>、=、<号)
①1221; ②2332; ③3443; ④4554; ⑤5665;…
(2)、从第(1)小题的结果经过归纳,可以猜想,nn+1和(n+1)n的大小关系是什么?(3)、根据上面归纳猜想得到的一般结论,可以猜想得到2007200820082007(填>、=、<).20. 观察下面的等式:回答下列问题:
(1)、填空: ;(2)、已知 ,则 的值是;(3)、设满足上面特征的等式最左边的数为 ,则 的最大值是 , 此时的等式为 .21. 快递员小王下午骑摩托车从总部出发,在一条东西走向的街道上来回收送包裹.他行驶的情况记录如下(向东记为“ ”,向西记为“ ”,单位:千米):, , , , , ,
(1)、小王最后是否回到了总部?(2)、小王离总部最远是多少米?在总部的什么方向?(3)、如果小王每走 米耗油 毫升,那么小王下午骑摩托车一共耗油多少毫升?22. 底边长为6厘米,高为9厘米的等腰三角形20个,迭放如图: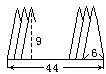
每两个等腰三角形有等距离的间隔,底边迭合在一起的长度是44厘米.回答下列问题:
(1)、两个三角形的间隔距离;(2)、三个三角形重叠(两次)部分的面积之和;(3)、只有两个三角形重叠(一次)部分的面积之和;(4)、迭到一起的总面积.