人教新课标A版必修二第四章圆与方程

试卷更新日期：2020-07-31 类型：单元试卷

进入出卷网下载

一、单选题

1. 过点A（1，2）作圆x²+（y﹣1）²＝1的切线，则切线方程是（）

A、x＝1 B、y＝2 C、x＝2或y＝1 D、x＝1或y＝2

查看试题解析
2. 已知直线 $x + y = 0$ 与圆 ${(x - 1)}^{2} + {(y - b)}^{2} = 2$ 相切，则 $b =$ （）

A、 $- 3$ B、 $1$ C、 $- 3$ 或 $1$ D、 $\frac{5}{2}$

查看试题解析
3. 圆 $x^{2} - 4 x + y^{2} = 0$ 与圆 $x^{2} + y^{2} + 4 x + 3 = 0$ 的公切线共有（）

A、1条 B、2条 C、3条 D、4条

查看试题解析
4. 圆 ${(x + 3)}^{2} + {(y + 4)}^{2} = 16$ 与圆 $x^{2} + y^{2} = 4$ 的位置关系为（）

A、相离 B、内切 C、外切 D、相交

查看试题解析
5. 已知点 $A (- 3, 1, 4)$ ，则点 $A$ 关于 $x$ 轴对称点的坐标为（）

A、 $(1, - 3, - 4)$ B、 $(- 3, - 1, - 4)$ C、 $(3, - 1, - 4)$ D、 $(4, - 1, 3)$

查看试题解析
6. 已知方程 $x^{2} + y^{2} + 2 x - y + m = 0$ 表示圆，则实数 $m$ 的取值范围是（）

A、 $m > \frac{5}{4}$ B、 $m > - \frac{5}{4}$ C、 $m < \frac{5}{4}$ D、 $m < - \frac{5}{4}$

查看试题解析
7. 直线 $2 x \cdot \sin θ + y = 0$ 被圆 $x^{2} + y^{2} - 2 \sqrt{5} y + 2 = 0$ 截得最大弦长为（）

A、 $2 \sqrt{5}$ B、 $2 \sqrt{3}$ C、3 D、 $2 \sqrt{2}$

查看试题解析
8. 若圆心坐标为 $(2, - 1)$ 的圆,被直线 $x - y - 1 = 0$ 截得的弦长为 $2 \sqrt{2}$ ，则这个圆的方程是（）

A、 ${(x - 2)}^{2} + {(y + 1)}^{2} = 2$ B、 ${(x - 2)}^{2} + {(y + 1)}^{2} = 4$ C、 ${(x - 2)}^{2} + {(y + 1)}^{2} = 8$ D、 ${(x - 2)}^{2} + {(y + 1)}^{2} = 16$

查看试题解析
9. 已知⊙M： $x^{2} + y^{2} - 2 x - 2 y - 2 = 0$ ，直线 $l$ ： $2 x + y + 2 = 0$ ，P为l上的动点，过点P作⊙M的切线 $P A, P B$ ，切点为 $A, B$ ，当 $| P M | \cdot | A B |$ 最小时，直线 $A B$ 的方程为（）

A、 $2 x - y - 1 = 0$ B、 $2 x + y - 1 = 0$ C、 $2 x - y + 1 = 0$ D、 $2 x + y + 1 = 0$

查看试题解析
10. 在平面直角坐标系 $x O y$ 中，矩形 $O A B C$ 的顶点坐标分别为 $O (0 ， 0) ， A (﹣ 4 ， 0) ， B (﹣ 4 ， 2) ， C (0 ， 2)$ ，则矩形 $O A B C$ 的外接圆方程是（）

A、 $x^{2} + y^{2} - 4 x + 2 y = 0$ B、 $x^{2} + y^{2} + 4 x - 2 y = 0$ C、 $x^{2} + y^{2} - 8 x + 4 y = 0$ D、 $x^{2} + y^{2} + 8 x - 4 y = 0$

查看试题解析
11. 已知平面 $A B C D ⊥$ 平面 $A D E F ， A B ⊥ A D ， C D ⊥ A D$ ，且 $A B = 3 ， A D = C D = 6 ， A D E F$ 是正方形，在正方形 $A D E F$ 内部有一点 $M$ ，满足 $M B ， M C$ 与平面 $A D E F$ 所成的角相等，则点 $M$ 的轨迹长度为（）

A、 $\frac{4}{3}$ B、16 C、 $\frac{4}{3} π$ D、 $8 π$

查看试题解析
12. 已知点 $P (t ， t - 1) ， t \in R$ ，点 $E$ 是圆 $x^{2} + y^{2} = \frac{1}{4}$ 上的动点，点 $F$ 是圆 ${(x - 3)}^{2} + {(y + 1)}^{2} = \frac{9}{4}$ 上的动点，则 $| P F | - | P E |$ 的最大值为（）

A、 $2$ B、 $\frac{5}{2}$ C、 $3$ D、 $4$

查看试题解析

二、多选题

13. 若圆 $C_{1} : {(x - 1)}^{2} + y^{2} = 1$ 与圆 $C_{2} : x^{2} + y^{2} - 8 x + 8 y + m = 0$ 相切，则m的值可以是（）

A、 $16$ B、 $7$ C、 $- 4$ D、 $- 7$

查看试题解析
14. 已知圆 $C : x^{2} + y^{2} + 2 m x - 2 (m + 1) y + 2 m^{2} + 2 m - 3 = 0 (m \in R)$ 上存在两个点到点 $A (0, - 1)$ 的距离为 $4$ ，则m的可能的值为（）

A、1 B、-1 C、-3 D、-5

查看试题解析
15. 已知 $P, Q$ 分别为圆M： ${(x - 6)}^{2} + {(y - 3)}^{2} = 4$ 与圆 $N$ ： ${(x + 4)}^{2} + {(y - 2)}^{2} = 1$ 上的动点，A为x轴上的动点，则 $| A P | + | A Q |$ 的值可能是（）

A、7 B、8 C、9 D、10

查看试题解析

三、填空题

16. 圆心在直线 $y = - 4 x$ ，且与直线 $x + y - 1 = 0$ 相切于点 $P (3 ， - 2)$ 的圆的标准方程为.

查看试题解析
17. 已知直线 $l$ 过点 $(- 1, 0)$ 且与直线 $2 x - y = 0$ 垂直，则圆 $x^{2} + y^{2} - 4 x + 8 y = 0$ 与直线 $l$ 相交所得的弦长为。

查看试题解析
18. 已知圆 $O ： x^{2} + y^{2} = 4$ ，直线 $l$ 与圆 $O$ 交于 $P ， Q$ 两点， $A (2 ， 2)$ ，若 $A P^{2} + A Q^{2} = 40$ ，则弦 $P Q$ 的长度的最大值为.

查看试题解析
19. 已知 $O$ 为坐标原点，圆 $M$ ： ${(x + 1)}^{2} + y^{2} = 1$ ，圆 $N$ ： ${(x - 2)}^{2} + y^{2} = 4$ ． $A ， B$ 分别为圆 $M$ 和圆 $N$ 上的动点，则 $S_{△ O A B}$ 的最大值为．

查看试题解析

四、解答题

20. 如图，正四棱锥P－ABCD中，底面边长为2，侧棱长为 $\sqrt{6}$ ，M ， N分别为AB ， BC的中点，以O为原点，射线OM ， ON ， OP分别为x轴、y轴、z轴的正方向建立空间直角坐标系．若E ， F分别为PA ， PB的中点，求A ， B ， C ， D ， E ， F的坐标．

查看试题解析
21. 已知圆 $C$ 的方程为： $x^{2} + y^{2} - 2 x - 4 y + m = 0$ .

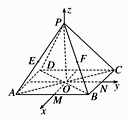(1)、求实数 $m$ 的取值范围；

(2)、若直线 $x - 2 y - 1 = 0$ 与圆 $C$ 相切，求实数 $m$ 的值.

查看试题解析
22. 分别根据下列条件，求圆的方程：

(1)、过点 $A (- 4, 0), B (0, 2)$ 和原点；

(2)、与两坐标轴均相切，且圆心在直线 $2 x - 3 y + 5 = 0$ 上.

查看试题解析
23. 已知圆C的圆心在坐标原点，且过点M（ $1, \sqrt{3}$ ）．

(1)、求圆C的方程；

(2)、已知点P是圆C上的动点，试求点P到直线 $x + y - 4 = 0$ 的距离的最小值；

查看试题解析
24. 已知直线 $l : x + y - 2 = 0$ 及圆 $C : {(x - 1)}^{2} + {(y - 2)}^{2} = 4$ ．

(1)、判断直线 $l$ 与圆 $C$ 的位置关系；

(2)、求过点 $(3, 1)$ 的圆 $C$ 的切线方程．

查看试题解析
25. 已知圆M：x²+y²-2y-4=0与圆N：x²+y²-4x+2y=0.

(1)、求证：两圆相交；

(2)、求两圆公共弦所在的直线方程及公共弦长；

(3)、在平面上找一点P，过点P引两圆的切线并使它们的长都等于1.

查看试题解析

人教新课标A版 必修二 第四章圆与方程

一、单选题

二、多选题

三、填空题

四、解答题

人教新课标A版必修二第四章圆与方程