人教新课标A版 必修二 第二章点、直线、平面之间的位置关系
试卷更新日期:2020-07-31 类型:单元试卷
一、单选题
-
1. 下列几何图形中,可能不是平面图形的是( )A、梯形 B、菱形 C、平行四边形 D、四边形2. 已知直线 平面 ,直线 ,则( )A、 B、 C、 异面 D、 相交而不垂直3. 在正方体 中, 与 是( )
 A、相交直线 B、平行直线 C、异面直线 D、相交且垂直的直线4. 已知 平面两两垂直,直线 满足: ,则直线 不可能满足以下哪种关系( )A、两两垂直 B、两两平行 C、两两相交 D、两两异面5. 已知 , 是空间内两条不同的直线, , 是空间内两个不同的平面,下列说法正确的是( )A、若 , ,则 B、若 , , ,则 C、若 , ,则 D、若 , , ,则6. 在长方体 中, ,则异面直线 与 所成角的余弦值为( )A、 B、 C、 D、7. 如图,正方体 中, , , , 分别为所在棱的中点,则下列各直线中,不与平面 平行的是( )
A、相交直线 B、平行直线 C、异面直线 D、相交且垂直的直线4. 已知 平面两两垂直,直线 满足: ,则直线 不可能满足以下哪种关系( )A、两两垂直 B、两两平行 C、两两相交 D、两两异面5. 已知 , 是空间内两条不同的直线, , 是空间内两个不同的平面,下列说法正确的是( )A、若 , ,则 B、若 , , ,则 C、若 , ,则 D、若 , , ,则6. 在长方体 中, ,则异面直线 与 所成角的余弦值为( )A、 B、 C、 D、7. 如图,正方体 中, , , , 分别为所在棱的中点,则下列各直线中,不与平面 平行的是( )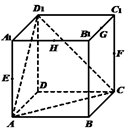 A、直线 B、直线 C、直线 D、直线8. 如图,在以下四个正方体中,使得直线 与平面 垂直的个数是( )
A、直线 B、直线 C、直线 D、直线8. 如图,在以下四个正方体中,使得直线 与平面 垂直的个数是( )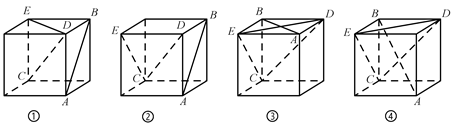 A、1 B、2 C、3 D、49. 三棱柱 中,底面边长和侧棱长都相等, ,则异面直线 与 所成角的余弦值为( )
A、1 B、2 C、3 D、49. 三棱柱 中,底面边长和侧棱长都相等, ,则异面直线 与 所成角的余弦值为( ) A、 B、 C、 D、10. 日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )
A、 B、 C、 D、10. 日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( ) A、20° B、40° C、50° D、90°11. 如图,在三棱柱 中,底面为正三角形,侧棱垂直底面, .若 分别是棱 上的点,且 , ,则异面直线 与 所成角的余弦值为( )
A、20° B、40° C、50° D、90°11. 如图,在三棱柱 中,底面为正三角形,侧棱垂直底面, .若 分别是棱 上的点,且 , ,则异面直线 与 所成角的余弦值为( ) A、 B、 C、 D、12. 在棱长均相等的正三棱柱 中, 为 的中点, 在 上,且 ,则下述结论:① ;② ;③平面 平面 :④异面直线 与 所成角为 其中正确命题的个数为( )
A、 B、 C、 D、12. 在棱长均相等的正三棱柱 中, 为 的中点, 在 上,且 ,则下述结论:① ;② ;③平面 平面 :④异面直线 与 所成角为 其中正确命题的个数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、多选题
-
13. 如图,平面α∩平面β=l,A,C是α内不同的两点,B,D是β内不同的两点,且A,B,C,D∉直线l,M,N分别是线段AB,CD的中点.下列判断正确的是( )
 A、若AB CD,则MN l B、若M,N重合,则AC l C、若AB与CD相交,且AC l,则BD可以与l相交 D、若AB与CD是异面直线,则MN不可能与l平行14. 在空间四边形 中, 分别是 上的点,当 平面 时,下面结论正确的是( )A、 一定是各边的中点 B、 一定是 的中点 C、 ,且 D、四边形 是平行四边形或梯形15. 如图所示,P为矩形 所在平面外一点,矩形对角线的交点为 为 的中点,给出以下结论,其中正确的是( )
A、若AB CD,则MN l B、若M,N重合,则AC l C、若AB与CD相交,且AC l,则BD可以与l相交 D、若AB与CD是异面直线,则MN不可能与l平行14. 在空间四边形 中, 分别是 上的点,当 平面 时,下面结论正确的是( )A、 一定是各边的中点 B、 一定是 的中点 C、 ,且 D、四边形 是平行四边形或梯形15. 如图所示,P为矩形 所在平面外一点,矩形对角线的交点为 为 的中点,给出以下结论,其中正确的是( )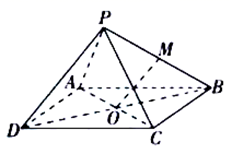 A、 B、 平面 C、 平面 D、 平面16. 如图,在正四棱柱 中, , , 分别为 , 的中点,异面直 与 所成角的余弦值为 ,则( )
A、 B、 平面 C、 平面 D、 平面16. 如图,在正四棱柱 中, , , 分别为 , 的中点,异面直 与 所成角的余弦值为 ,则( ) A、 B、直线 与直线 共面 C、 D、直线 与直线 异面
A、 B、直线 与直线 共面 C、 D、直线 与直线 异面三、填空题
-
17. 若直线 平面 ,直线 ,则 与 的位置关系是18. 下列说法中正确的有个.
①空间中三条直线交于一点,则这三条直线共面;
②一个平行四边形确定一个平面;
③若一个角的两边分别平行于另一个角的两边,则这两个角相等;
④已知两个不同的平面 和 ,若 , ,且 ,则点A在直线 上.
19. 如图所示,正方体ABCD﹣A1B1C1D1中,E,F分别是棱BC,CC1的中点,则异面直线EF与B1D1所成的角为. 20. 如图,已知圆柱的轴截面 是正方形,C是圆柱下底面弧 的中点, 是圆柱上底面弧 的中点,那么异面直线 与 所成角的正切值为.
20. 如图,已知圆柱的轴截面 是正方形,C是圆柱下底面弧 的中点, 是圆柱上底面弧 的中点,那么异面直线 与 所成角的正切值为.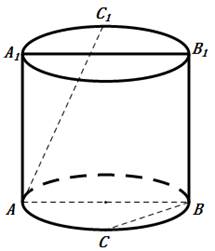
四、解答题
-
21. 如图,已知四棱锥 ,底面四边形 为正方形, ,M,N分别是线段 、 的中点.
 (1)、求证: ∥平面 ;(2)、求异面直线MN与BC所成角的大小.22. 如图,在长方体 中,点E,F分别在棱 , 上,且 , .证明:
(1)、求证: ∥平面 ;(2)、求异面直线MN与BC所成角的大小.22. 如图,在长方体 中,点E,F分别在棱 , 上,且 , .证明: (1)、当 时, ;(2)、点 在平面 内.23. 在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.
(1)、当 时, ;(2)、点 在平面 内.23. 在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.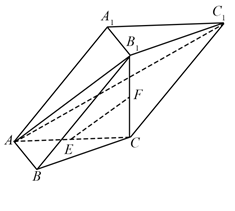 (1)、求证:EF∥平面AB1C1;(2)、求证:平面AB1C⊥平面ABB1 .
(1)、求证:EF∥平面AB1C1;(2)、求证:平面AB1C⊥平面ABB1 .


