人教新课标A版 必修二 2.3直线、平面垂直的判定及其性质
试卷更新日期:2020-07-31 类型:同步测试
一、单选题
-
1. 已知直线 平面 ,直线 ,则( )A、 B、 C、 异面 D、 相交而不垂直2. 已知三棱锥A-BCD中,AD⊥BC,AD⊥CD,则有( )A、平面ABC⊥平面ADC B、平面ADC⊥平面BCD C、平面ABC⊥平面BDC D、平面ABC⊥平面ADB3. 如图,在以下四个正方体中,使得直线 与平面 垂直的个数是( )
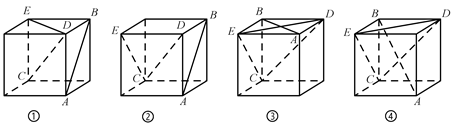 A、1 B、2 C、3 D、44. 如图,四棱锥 的底面为正方形, ,则下列结论中不正确的是( )
A、1 B、2 C、3 D、44. 如图,四棱锥 的底面为正方形, ,则下列结论中不正确的是( )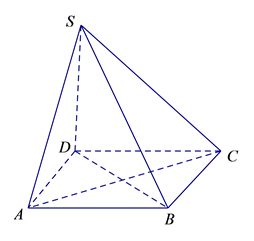 A、 B、 C、平面 平面 D、5. 已知三棱锥 中,若PA,PB,PC两两互相垂直,作 面ABC,垂足为O,则点O是 的( )A、外心 B、内心 C、重心 D、垂心6. 如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点, 平面ABC,则四面体 的四个面中,直角三角形的个数有( )
A、 B、 C、平面 平面 D、5. 已知三棱锥 中,若PA,PB,PC两两互相垂直,作 面ABC,垂足为O,则点O是 的( )A、外心 B、内心 C、重心 D、垂心6. 如图,AB是⊙O的直径,C是圆周上不同于A,B的任意一点, 平面ABC,则四面体 的四个面中,直角三角形的个数有( ) A、4个 B、3个 C、2个 D、1个7. 已知 是两条不同的直线, 是三个不同的平面,下列命题中:
A、4个 B、3个 C、2个 D、1个7. 已知 是两条不同的直线, 是三个不同的平面,下列命题中:①若 ,且 ∥ ,则 ∥ ;②若 相交,且都在 外, , ∥ , , ∥ ,则 ∥ ;③若 , , , ,则 ;④若 , , , ,则 .其中正确命题的序号是( )
A、①②③ B、①③ C、②③ D、①②③④8. 如图所示,在正方形 中, 分别是 的中点,现在沿 把这个正方形折成一个四面体,使 三点重合,重合后的点记为 .给出下列关系:① 平面 ;② 平面 ;③ ;④ 上平面 .其中关系成立的有( )
 A、①② B、①③ C、②③ D、③④9. 如图, 为圆 的直径, , 垂直于圆 所在的平面, 为圆周上不与点 、 重合的点, 于 , 于 ,则下列不正确的是( )
A、①② B、①③ C、②③ D、③④9. 如图, 为圆 的直径, , 垂直于圆 所在的平面, 为圆周上不与点 、 重合的点, 于 , 于 ,则下列不正确的是( ) A、平面 平面 B、平面 平面 C、平面 平面 D、平面 平面10. 如图,在正方形 中, 分别是 的中点, 是 的中点.现在沿 及 把这个正方形折成一个空间图形,使 三点重合,重合后的点记为 ,下列说法:
A、平面 平面 B、平面 平面 C、平面 平面 D、平面 平面10. 如图,在正方形 中, 分别是 的中点, 是 的中点.现在沿 及 把这个正方形折成一个空间图形,使 三点重合,重合后的点记为 ,下列说法: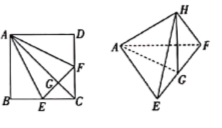
① 平面 ;② 平面 ;
③ 平面 ;④ 平面 .
其中正确的有( )
A、1个 B、2个 C、3个 D、4个11. 如图,已知 是顶角为 的等腰三角形,且 ,点 是 的中点.将 沿 折起,使得 ,则此时直线 与平面 所成角的正弦值为( )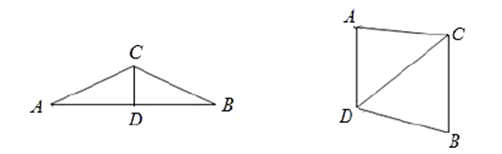 A、 B、 C、 D、12. 正四面体 的棱 与平面 所成角为 ,其中 ,点 在平面 内,则当四面体 转动时( )A、存在某个位置使得
A、 B、 C、 D、12. 正四面体 的棱 与平面 所成角为 ,其中 ,点 在平面 内,则当四面体 转动时( )A、存在某个位置使得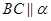 ,也存在某个位置使得
,也存在某个位置使得  B、存在某个位置使得
B、存在某个位置使得 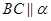 ,但不存在某个位置使得
,但不存在某个位置使得  C、不存在某个位置使得
C、不存在某个位置使得 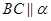 ,但存在某个位置使得
,但存在某个位置使得  D、既不存在某个位置使得
D、既不存在某个位置使得 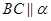 ,也不存在某个位置使得
,也不存在某个位置使得 
二、填空题
-
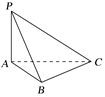
13. 如图,△ABC是直角三角形,∠ABC=90°,PA⊥平面ABC,则此图形中有个直角三角形.
 14. 如图所示,四棱锥 的底面 是边长为 的正方形,侧棱 , ,则它的5个面中,互相垂直的面有对.
14. 如图所示,四棱锥 的底面 是边长为 的正方形,侧棱 , ,则它的5个面中,互相垂直的面有对.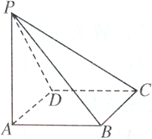 15. 如图甲所示,在直角 中, , 是垂足,则有 ,该结论称为射影定理.如图乙所示,在三棱锥 中, 平面 , 平面 , 为垂足,且 在 内,类比直角三角形中的射影定理,则有 .
15. 如图甲所示,在直角 中, , 是垂足,则有 ,该结论称为射影定理.如图乙所示,在三棱锥 中, 平面 , 平面 , 为垂足,且 在 内,类比直角三角形中的射影定理,则有 .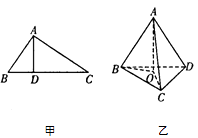 16. 如图,在棱长为1的正方体 中,点E、F是棱 、 的中点,P是底面 上(含边界)一动点,满足 ,则线段 长度的最小值为.
16. 如图,在棱长为1的正方体 中,点E、F是棱 、 的中点,P是底面 上(含边界)一动点,满足 ,则线段 长度的最小值为.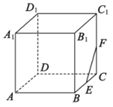
三、解答题
-
17. 如图所示,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点,
求证:平面PAC⊥平面PBC.
 18. 如图长方体ABCD-A1B1C1D1中,AB= AD,E,F分别为棱AB,A1D1的中点
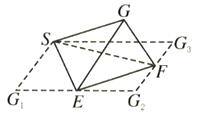
18. 如图长方体ABCD-A1B1C1D1中,AB= AD,E,F分别为棱AB,A1D1的中点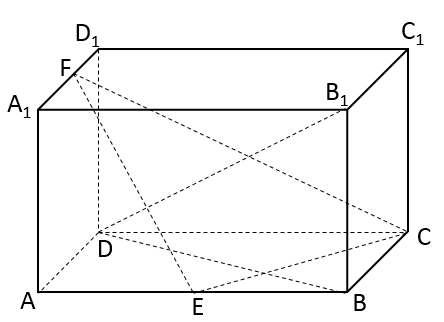 (1)、求证:平面EFC⊥平面BB1D;(2)、请在答题卡图形中画出直线DB1与平面EFC的交点O(保留必要的辅助线),写出画法并计算 的值(不必写出计算过程)19. 图1是由矩形ADEB、 ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB , BC折起使得BE与BF重合,连结DG , 如图2.
(1)、求证:平面EFC⊥平面BB1D;(2)、请在答题卡图形中画出直线DB1与平面EFC的交点O(保留必要的辅助线),写出画法并计算 的值(不必写出计算过程)19. 图1是由矩形ADEB、 ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB , BC折起使得BE与BF重合,连结DG , 如图2.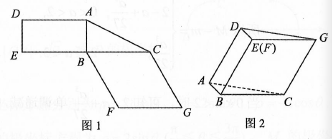 (1)、证明图2中的A , C , G , D四点共面,且平面ABC⊥平面BCGE;(2)、求图2中的四边形ACGD的面积.20. 如图,正方形 所在的平面与 所在的平面相交于 , ⊥平面 ,且 .
(1)、证明图2中的A , C , G , D四点共面,且平面ABC⊥平面BCGE;(2)、求图2中的四边形ACGD的面积.20. 如图,正方形 所在的平面与 所在的平面相交于 , ⊥平面 ,且 . (1)、求证: ⊥平面 ;(2)、求 到正方形 所在平面的距离.
(1)、求证: ⊥平面 ;(2)、求 到正方形 所在平面的距离.