内蒙古赤峰市2019-2020学年高一上学期数学联合考试试卷
试卷更新日期:2020-07-31 类型:月考试卷
一、单选题
-
1. 已知集合 , ,则 ( )A、{5} B、 C、 D、2. 若 ,且 ( ,且 ),则a可能的取值为( )A、 B、 C、 D、3. 已知函数 ,则 ( )A、 B、4 C、 D、4. 若函数 的定义域为 ,则函数 的定义域为( )A、 B、 C、 D、5. 已知某停车场规定:停车时间在3小时内,车主需交费5元,若停车超过3小时,每多停1小时,车主要多交3元,不足1小时按1小时计算.一辆汽车在该停车场停了7小时20分钟,在离开时车主应交的停车费为( )A、16元 B、18元 C、20元 D、22元6. 下列函数既是奇函数又是减函数的是( )A、 B、 C、 D、7. 函数 的零点 所在区间为( )A、 B、 C、 D、8. 函数f(x)=x2+ 的图象大致为( )A、
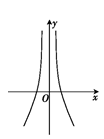 B、
B、 C、
C、 D、
D、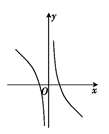 9. 设 ,则 的大小关系为( )A、 B、 C、 D、10. 若函数 满足 ,则 在 上的值域为( )A、 B、 C、 D、11. 已知函数 在 上的最大值为 ,则m的取值范围是( )A、 B、 C、 D、12. 已知函数 ,则不等式 的解集为( )A、 B、 C、 D、
9. 设 ,则 的大小关系为( )A、 B、 C、 D、10. 若函数 满足 ,则 在 上的值域为( )A、 B、 C、 D、11. 已知函数 在 上的最大值为 ,则m的取值范围是( )A、 B、 C、 D、12. 已知函数 ,则不等式 的解集为( )A、 B、 C、 D、二、填空题
-
13. 已知函数 ,若 ,则 .14. 已知奇函数 的定义域为 ,且在 上单调递减,则不等式 的解集为.15. 若函数 ( ,且 )有最大值,且最大值不小于-1,则a的取值范围为.
三、双空题
-
16. 用“ ”“ ”“ ”“ ”填空:0 , .
四、解答题
-
17. 设集合 , , .(1)、求 , ;(2)、若 ,求 ;(3)、若 ,求 的取值范围.18.(1)、求值 ;(2)、求值 .19. 已知函数(1)、判断 在 上的单调性(不需要证明);(2)、若 在 上为单调函数,求a的取值范围.20. 尽管目前人类还无法准确预报地震,但科学家通过研究,已经对地震有所了解,例如,地震释放出的能量 (单位:焦耳)与地震里氏震级 之间的关系为 .(1)、已知地震等级划分为里氏 级,根据等级范围又分为三种类型,其中小于 级的为“小地震”,介于 级到 级之间的为“有感地震”,大于 级的为“破坏性地震”若某次地震释放能量约 焦耳,试确定该次地震的类型;(2)、2008年汶川地震为里氏 级,2011年日本地震为里氏 级,问:2011年日本地震所释放的能量是2008年汶川地震所释放的能量的多少倍? (取 )
-