2020年暑期衔接训练青岛版数学八年级下册：第21讲 图形的平移与旋转
试卷更新日期：2020-07-31 类型：单元试卷
一、单选题
-
1. 如图，△ABC沿BC所在直线向左平移4cm得到△A'B'C'，若△ABC的周长为20cm，则四边形A'B'CA的周长为（ ）
A、16cm B、24cm C、28cm D、32cm2. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
3. 如图， 与 关于点O成中心对称，下列说法：①∠BAC= C，②AC= ，③OA=O ，④ ABC与 的面积相等，其中正确的有（ ）.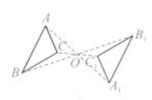
A、1个 B、2个 C、3个 D、4个4. 如图，在平面直角坐标系xOy中，将四边形ABCD先向下平移，再向右平移得到四边形A1B1C1D1 ， 已知A（-3，5)，B(-4，3)，A1(3，3)，则B1的坐标为（ ）
A、(1，2) B、(1，4) C、(2，1) D、(4，1)5. 下列图形中，绕某个点旋转180°能与自身重合的图形有（ ）①正方形；②等边三角形；③长方形；④角；⑤平行四边形；⑥圆
A、2个 B、3个 C、4个 D、5个6. 如图，△DEF是由△ABC绕着某点旋转得到的，则这点的坐标是（ ）
A、（1，1） B、（0，1） C、（﹣1，1） D、（2，0）7. 一辆模型赛车，先前进1m，然后沿原地逆时针方向旋转，旋转角为a(0<a<90°)，被称为一次操作，若五次操作后，发现赛车回到出发点，则旋转角a为（ ）A、108° B、120° C、72 ° D、36°8. 如图，已知两个全等直角三角形的直角顶点及一条直角边重合，将△ABC绕点C按顺时针方向旋转到△A′CB′的位置，其中A′C交直线AD于点E，A′B′分别交直线AD，AC于点F，G．则旋转后的图中，全等三角形共有（ ）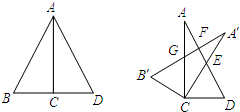
A、2对 B、3对 C、4对 D、5对9. 如图，由4个小正方形组成的田字格中，△ABC的顶点都是小正方形的顶点，在田字格上画与△ABC成轴对称的三角形，且顶点都是小正方形的顶点，则这样的三角形的个数有(不包含△ABC本身)（ ）
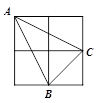A、4个 B、3个 C、2个 D、1个10. 如图，直角三角形ABC的直角边AB=6，BC=8，将直角三角形ABC沿边BC的方向平移到三角形DEF的位置，DE交AC于点G ， BE=2，三角形CEG的面积为13.5，下列结论：①三角形ABC平移的距离是4；②EG=4.5；③AD∥CF；④四边形ADFC的面积为6．其中正确的结论是
A、①② B、②③ C、③④ D、②④11. 如图，在平面直角坐标系xOy中，有一个等腰直角三角形AOB，∠OAB＝90°，直角边AO在x轴上，且AO＝1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1 ， 且A1O＝2AO，再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2 ， 且A2O＝2A1O……依此规律，得到等腰直角三角形A2 017OB2 017.则点B2 017的坐标（ ）
A、（22 017 ， －22 017） B、（22 016 ， －22 016） C、（22 017 ， 22 017） D、（22 016 ， 22 016）12. 有两个全等的含30°角的直角三角板重叠在一起，如图，将△A′B′C′绕AC的中点M转动，斜边A′B′刚好过△ABC的直角顶点C，且与△ABC的斜边AB交于点N，连接AA′、C′C、AC′．若AC的长为2，有以下五个结论：①AA′=1；②C′C⊥A′B′；③点N是边AB的中点；④四边形AA′CC′为矩形；⑤A′N=B′C= ，其中正确的有（ ）
A、2个 B、3个 C、4个 D、5个二、填空题
-
13. 如图，楼梯的长为5m，高为3m，计划在楼表面铺地毯，地毯的长度至少需要 m．
14. 如图，将 沿 方向平移得到 ，如果 ， ， ，那么图中阴影部分的面积为
15. 如图，将△ABC绕点 旋转到△AEF的位置，点E在BC边上，EF与AC交于点G.若∠B＝70°，∠C＝25°，则∠FGC＝°.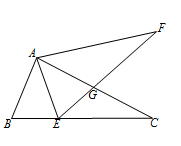
16. 如图，直线a、b垂直相交于点O，曲线C关于点O成中心对称，点A的对称点是点A'，AB⊥a于点B，A'D⊥b于点D．若OB＝3，OD＝2，则阴影部分的面积之和为 ．
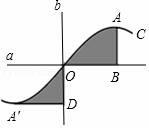17. 如图，在平面直角坐标系中，点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O'A'B，点A的对应点A'是直线y= x上一点，则点B与其对应点B'间的距离为.
18. 如图，在 中， ， ， ， 可以由 绕点C顺时针旋转得到，其中点 与点A是对应点，点 与点B是对应点，连接 ，且A、 、 在同一条直线上，则 的长为 ．
19. 如图，将n个边长都为1cm的正方形按如图所示摆放，点A1， A2，…，An分别是正方形的中心，则n个正方形重叠形成的重叠部分的面积和为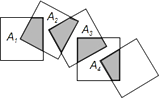
20. 如图，在直角坐标系中，已知点A（﹣3，0）、B（0，4），对△OAB连续作旋转变换，依次得到△1、△2、△3、△4…，则△2013的直角顶点的坐标为.
三、作图题
-
21. 在平面直角坐标系中， 的位置如图所示（每个小方格都是边长1个单位长度的正方形）.
(1)、将 沿 轴方向向左平移6个单位，画出平移后得到的 .(2)、将 绕着点 顺时针旋转 ，画出旋转后得到的 ；直接写出点 的坐标.(3)、作出 关于原点 成中心对称的 ，并直接写出 的坐标.四、解答题
-
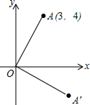
22. 在平面直角坐标系 中， 点的坐标为 ，将 绕原点 顺时针旋转 得到 ，求点 的坐标．
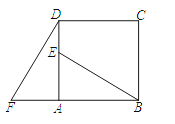
23. 如图，在等边△ABC内有一点P，且PA=2，PB= ，PC=1，求∠BPC的度数和等边△ABC的边长．
24.如图，四边形ABCD是正方形，E是AD上任意一点，延长BA到F，使得AF=AE，连接DF：
（1）旋转△ADF可得到哪个三角形？
（2）旋转中心是哪一点？旋转了多少度？
（3）BE与DF的数量关系、位置关系如何？为什么？
25. 把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起(如图1)，且使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合，现将三角板EFG绕O点顺时针旋转，旋转角 满足条件 四边形CHGK是旋转过程中两三角板的重叠部分(如图2).
(1)、在上述旋转过程中，BH与CK有怎样的数量关系？证明你的结论；(2)、在上述旋转过程中，两个直角三角形的重叠部分面积是否会发生改变？证明你的结论.26. 如图①，在△ABC中，AB=AC，D是射线BC上一点(点D不与点B重合)，连结AD，将AD绕着点A逆时针旋转∠BAC的度数得到AE，连结DE、CE。
(1)、当点D在边BC上，求证：△BAD≌△CAE。(2)、当点D在边BC上，若∠BAC=a，求∠DCE的大小．(用含a的代数式表示)。(3)、当DE与△ABC的边所在的直线垂直，且∠BAC=40°时，请借助图②，直接写出∠CED的大小。
-
