人教新课标A版必修二 2.1空间点、直线、平面之间的位置关系

试卷更新日期：2020-07-31 类型：同步测试

进入出卷网下载

一、单选题

1. 不重合的两个平面可以把空间分成（）部分

A、2 B、3或4 C、4 D、2或3或4

查看试题解析
2. 如果两条直线a与b没有公共点，那么a与b（）

A、共面 B、平行 C、异面 D、平行或异面

查看试题解析
3. 下列条件能唯一确定一个平面的是（）

A、空间任意三点 B、不共线三点 C、共线三点 D、两条异面直线

查看试题解析
4. 下列几何图形中，可能不是平面图形的是（）

A、梯形 B、菱形 C、平行四边形 D、四边形

查看试题解析
5. 已知直线m⊄平面α，直线n⊂平面α，且点A∈直线m，点A∈平面α，则直线m，n的位置关系不可能是（）

A、垂直 B、相交 C、异面 D、平行

查看试题解析
6. 如图所示，平面 $α \cap$ 平面 $β = l$ ，点 $A ， B \in α$ ，点 $C \in β$ ，直线 $A B \cap l = R$ .设过 $A ， B ， C$ 三点的平面为 $γ$ ，则 $β \cap γ =$ （）

A、直线 $A C$ B、直线 $B C$ C、直线 $C R$ D、以上均不正确

查看试题解析
7. 在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $B D_{1}$ 与 $B_{1} C$ 是（）

A、相交直线 B、平行直线 C、异面直线 D、相交且垂直的直线

查看试题解析
8. 在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A D = 3 ， A A_{1} = A B = 4$ ，则异面直线 $A_{1} B$ 与 $A C$ 所成角的余弦值为（）

A、 $\frac{\sqrt{2}}{5}$ B、 $\frac{2}{5}$ C、 $\frac{2 \sqrt{2}}{5}$ D、 $\frac{4}{5}$

查看试题解析
9. 三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，底面边长和侧棱长都相等， $∠ B A A_{1} = ∠ C A A_{1} = 60^{°}$ ，则异面直线 $A B_{1}$ 与 $B C_{1}$ 所成角的余弦值为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{\sqrt{6}}{6}$ C、 $\frac{\sqrt{3}}{4}$ D、 $\frac{\sqrt{3}}{6}$

查看试题解析
10. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的八个顶点中任取两个点作直线，与直线 $A_{1} B$ 异面且夹角成 $60 °$ 的直线的条数为（）．

A、 $3$ B、 $4$ C、 $5$ D、 $6$

查看试题解析
11. 如图所示， $A B C D - A_{1} B_{1} C_{1} D_{1}$ 是长方体， $O$ 是 $B_{1} D_{1}$ 的中点，直线 $A_{1} C$ 交平面 $A B_{1} D_{1}$ 于点 $M$ ，则下列结论正确的是（）

A、 $A ， M ， O$ 三点共线 B、 $A ， M ， O ， A_{1}$ 不共面 C、 $A ， M ， C ， O$ 不共面 D、 $B ， B_{1} ， O ， M$ 共面

查看试题解析
12. 如图，在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，底面为正三角形，侧棱垂直底面， $A B = 4 ， A A_{1} = 8$ .若 $E ， F$ 分别是棱 $B B_{1} ， C C$ 上的点，且 $B E = B_{1} E$ ， $C_{1} F = \frac{1}{4} C C_{1}$ ，则异面直线 $A_{1} E$ 与 $A F$ 所成角的余弦值为（）

A、 $\frac{\sqrt{2}}{10}$ B、 $\frac{\sqrt{26}}{13}$ C、 $\frac{\sqrt{13}}{13}$ D、 $\frac{\sqrt{13}}{10}$

查看试题解析

二、填空题

13. 若直线a、b均平行于平面 $α$ ，那么a与b位置关系是

查看试题解析
14. 下列说法中正确的有个.
①空间中三条直线交于一点，则这三条直线共面；

②一个平行四边形确定一个平面；

③若一个角的两边分别平行于另一个角的两边，则这两个角相等；

④已知两个不同的平面 $α$ 和 $β$ ，若 $A \in α$ ， $A \in β$ ，且 $α \cap β = l$ ，则点A在直线 $l$ 上.

查看试题解析
15. 如图所示，正方体ABCD﹣A₁B₁C₁D₁中，E，F分别是棱BC，CC₁的中点，则异面直线EF与B₁D₁所成的角为.

查看试题解析
16. 如图，已知圆柱的轴截面 $A B B_{1} A_{1}$ 是正方形，C是圆柱下底面弧 $A B$ 的中点， $C_{1}$ 是圆柱上底面弧 $A_{1} B_{1}$ 的中点，那么异面直线 $A C_{1}$ 与 $B C$ 所成角的正切值为.

查看试题解析

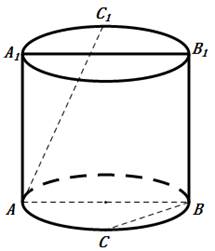
三、解答题

17.

(1)、用符号表示下来语句，并画出同时满足这四个语句的一个几何图形：
①直线 $l$ 在平面 $α$ 内；

②直线m不在平面 $α$ 内；

③直线m与平面 $α$ 交于点A；

④直线l不经过点A.

(2)、如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ 为棱 $B B_{1}$ 的中点，F为棱 $C C_{1}$ 的三等分点，画出由 $D_{1} ， E ， F$ 三点所确定的平面 $β$ 与平面 $A B C D$ 的交线.(保留作图痕迹)

查看试题解析
18. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ ， $F$ 分别为 $D_{1} C_{1}$ ， $C_{1} B_{1}$ 的中点， $A C \cap B D = P$ ， $A_{1} C_{1} \cap E F = Q$ 求证：

(1)、 $D ， B ， F ， E$ 四点共面

(2)、若 $A_{1} C_{1}$ 交平面 $D B E F$ 于R 点，则 $P ， Q ， R$ 三点共线．

查看试题解析
19. 如图，已知点 $E ， F ， G ， H$ 分别为正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱 $A B ， B C ， C C_{1} ， C_{1} D_{1}$ 的中点，求证： $E F ， H G ， D C$ 三线共点．

查看试题解析
20. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，E、F、G、H分别是棱 $A B$ 、 $B C$ 、 $C C_{1}$ 、 $C_{1} D_{1}$ 的中点.

(1)、判断直线 $E F$ 与 $G H$ 的位置关系，并说明理由；

(2)、求异面直线 $A_{1} D$ 与 $E F$ 所成的角的大小.

查看试题解析
21. 如图，四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为矩形， $P A ⊥$ 底面 $A B C D$ ， $A B = P A = 1$ ， $A D = \sqrt{3}$ ， $F ， F$ 分别为棱 $P D ， P A$ 的中点.

(1)、求证： $B$ 、 $C$ 、 $E$ 、 $F$ 四点共面；

(2)、求异面直线 $P B$ 与 $A E$ 所成的角.

查看试题解析
22.

(1)、已知四棱锥 $P - A B C D$ 的侧棱长与底面边长都相等，四边形 $A B C D$ 为正方形，点 $E$ 是 $P B$ 的中点，求异面直线 $A E$ 与 $P D$ 所成角的余弦值．

(2)、如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A A_{1} = 1 ， A B = A D = 2 ， E ， F$ 分别是 $B C ， D C$ 的中点，求异面直线 $A D_{1}$ 与 $E F$ 所成角的余弦值．

查看试题解析

人教新课标A版 必修二 2.1空间点、直线、平面之间的位置关系

一、单选题

二、填空题

三、解答题

人教新课标A版必修二 2.1空间点、直线、平面之间的位置关系