人教新课标A版 必修二 第一章空间几何体
试卷更新日期:2020-07-31 类型:单元试卷
一、单选题
-
1. 下列命题中正确的有( )
①一个棱柱至少有5个平面;②正棱锥的侧面都是全等的等腰三角形;③有两个面平行且相似,其他各面都是梯形的多面体是棱台;④正方形的直观图是正方形;
A、1 B、2 C、3 D、42. 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图所示,是一个正方体的表面展开图,若图中“2”在正方体的上面,则这个正方体的下面是( ) A、0 B、9 C、快 D、乐3. 某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为( ).
A、0 B、9 C、快 D、乐3. 某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为( ).
A、 B、 C、 D、4. 若圆锥的高等于底面直径,则它的底面积与侧面积之比为( )A、1∶2 B、1∶ C、1∶ D、 ∶25. 若棱长为 的正方体的顶点都在同一球面上,则该球的表面积为( )A、 B、 C、 D、6. 已知高为3的棱柱 的底面是边长为1的正三角形(如图),则三棱锥 的体积为( )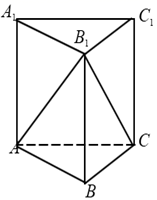 A、 B、 C、 D、7. 如图, 是水平放置的 的直观图, , ,则 的面积是( )
A、 B、 C、 D、7. 如图, 是水平放置的 的直观图, , ,则 的面积是( )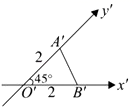 A、2 B、3 C、4 D、58. 如果两个球的体积之比为 ,那么两个球的半径之比为( )A、 B、 C、 D、9. 如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M,在俯视图中对应的点为N,则该端点在侧视图中对应的点为( )
A、2 B、3 C、4 D、58. 如果两个球的体积之比为 ,那么两个球的半径之比为( )A、 B、 C、 D、9. 如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M,在俯视图中对应的点为N,则该端点在侧视图中对应的点为( )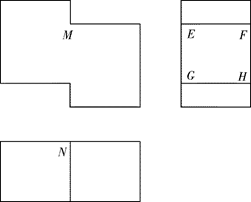 A、E B、F C、G D、H10. 我国古代数学名著《九章算术》对立体几何也有深入的研究,从其中的一些数学用语可见,譬如“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.现有一如图所示的“堑堵”即三棱柱 ,其中 ,若 ,当“阳马”即四棱锥 体积最大时,“堑堵”即三棱柱 的表面积为( )
A、E B、F C、G D、H10. 我国古代数学名著《九章算术》对立体几何也有深入的研究,从其中的一些数学用语可见,譬如“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.现有一如图所示的“堑堵”即三棱柱 ,其中 ,若 ,当“阳马”即四棱锥 体积最大时,“堑堵”即三棱柱 的表面积为( )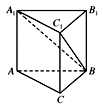 A、 B、 C、 D、11. 已知棱长为2的正方体 中,E为DC中点,F在线段 上运动,则三棱锥 的外接球的表面积最小值为( )A、 B、 C、 D、12. 如图,棱长为l的正方体 中,P为线段 的中点, 分别为线段 和 棱 上任意一点,则 的最小值为( )
A、 B、 C、 D、11. 已知棱长为2的正方体 中,E为DC中点,F在线段 上运动,则三棱锥 的外接球的表面积最小值为( )A、 B、 C、 D、12. 如图,棱长为l的正方体 中,P为线段 的中点, 分别为线段 和 棱 上任意一点,则 的最小值为( )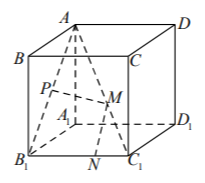 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
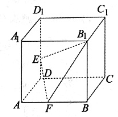
13. 已知正四棱柱底面边长为 ,体积为32,则此四棱柱的表面积为14. 已知某正四棱锥的底面边长和侧棱长均为 ,则该棱锥的体积为 .15. 已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为 .16. 如图,正方体 的棱长为1,E为棱 上的点, 为AB的中点,则三棱锥 的体积为.
三、解答题
-
17. 如图,正方形 的边长为1cm,它是水平放置的一个平面图形的直观图.请画出原来的平面图形的形状,并求原图形的周长与面积.
 18. 已知一个长方体共一顶点的三个面的面积分别是 、 、 ,(1)、求这个长方体的对角线长。(2)、求这个长方体的的体积19. 如图所示,四棱锥V-ABCD的底面为边长等于2的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长均为4,求这个四棱锥的体积及表面积.
18. 已知一个长方体共一顶点的三个面的面积分别是 、 、 ,(1)、求这个长方体的对角线长。(2)、求这个长方体的的体积19. 如图所示,四棱锥V-ABCD的底面为边长等于2的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长均为4,求这个四棱锥的体积及表面积. 20.(1)、某圆锥的侧面展开图为圆心角为 ,面积为 的扇形,求该圆锥的表面积和体积.(2)、已知直三棱柱 的底面是边长为 的正三角形,且该三棱柱的外接球的表面积为 ,求该三棱柱的体积.
20.(1)、某圆锥的侧面展开图为圆心角为 ,面积为 的扇形,求该圆锥的表面积和体积.(2)、已知直三棱柱 的底面是边长为 的正三角形,且该三棱柱的外接球的表面积为 ,求该三棱柱的体积.