人教新课标A版 必修二 1.3空间几何体的表面积与体积
试卷更新日期:2020-07-31 类型:同步测试
一、单选题
-
1. 一个正四棱锥的底面边长为2,高为 ,则该正四棱锥的全面积为( )A、8 B、12 C、16 D、202. 已知一个四棱锥的高为3,其底面用斜二测画法所画出的水平放置的直观图是一个边长为1的正方形,则此四棱锥的体积为( )A、 B、 C、 D、3. 如果两个球的体积之比为 ,那么两个球的半径之比为( )A、 B、 C、 D、4. 若棱长为 的正方体的顶点都在同一球面上,则该球的表面积为( )A、 B、 C、 D、5. 已知正方体外接球的体积是 π,那么正方体的棱长等于( )A、2 B、 C、 D、6. 已知某圆锥的表面积是14π,其侧面展开图是顶角为 的扇形,则该圆锥的侧面积为( )A、π B、2π C、6π D、12π7. 已知高为3的棱柱 的底面是边长为1的正三角形(如图),则三棱锥 的体积为( )
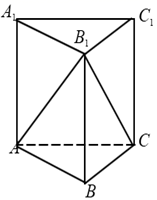 A、 B、 C、 D、8. 在四面体 中,棱 ,其余各条棱长均为2,则四面体 外接球的表面积是( )A、 B、 C、 D、9. 某几何体的三视图如图所示,则该几何体的体积V=( )
A、 B、 C、 D、8. 在四面体 中,棱 ,其余各条棱长均为2,则四面体 外接球的表面积是( )A、 B、 C、 D、9. 某几何体的三视图如图所示,则该几何体的体积V=( ) A、 B、 C、 D、10. 已知棱长为2的正方体 中,E为DC中点,F在线段 上运动,则三棱锥 的外接球的表面积最小值为( )A、 B、 C、 D、11. 在高为 的正三棱柱 中, 的边长为2, 为棱 的中点,若一只蚂蚁从点 沿表面爬向点 ,则蚂蚁爬行的最短距离为( )A、3 B、 C、 D、212. 我国古代数学名著《九章算术》对立体几何也有深入的研究,从其中的一些数学用语可见,譬如“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.现有一如图所示的“堑堵”即三棱柱 ,其中 ,若 ,当“阳马”即四棱锥 体积最大时,“堑堵”即三棱柱 的表面积为( )
A、 B、 C、 D、10. 已知棱长为2的正方体 中,E为DC中点,F在线段 上运动,则三棱锥 的外接球的表面积最小值为( )A、 B、 C、 D、11. 在高为 的正三棱柱 中, 的边长为2, 为棱 的中点,若一只蚂蚁从点 沿表面爬向点 ,则蚂蚁爬行的最短距离为( )A、3 B、 C、 D、212. 我国古代数学名著《九章算术》对立体几何也有深入的研究,从其中的一些数学用语可见,譬如“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥.现有一如图所示的“堑堵”即三棱柱 ,其中 ,若 ,当“阳马”即四棱锥 体积最大时,“堑堵”即三棱柱 的表面积为( )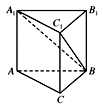 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
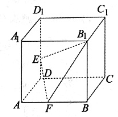
13. 已知某正四棱锥的底面边长和侧棱长均为 ,则该棱锥的体积为 .14. 已知圆柱的底面直径和高都等于球的直径,则球与圆柱的表面积之比为.15. 已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为 .16. 如图,正方体 的棱长为1,E为棱 上的点, 为AB的中点,则三棱锥 的体积为.
三、解答题
-
17. 已知一个长方体共一顶点的三个面的面积分别是 、 、 ,(1)、求这个长方体的对角线长。(2)、求这个长方体的的体积18. 底面边长为2的正三棱锥 ,其表面展开图是三角形 ,如图,求△ 的各边长及此三棱锥的体积 .
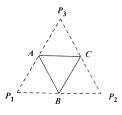 19.(1)、某圆锥的侧面展开图为圆心角为 ,面积为 的扇形,求该圆锥的表面积和体积.(2)、已知直三棱柱 的底面是边长为 的正三角形,且该三棱柱的外接球的表面积为 ,求该三棱柱的体积.20. 如图,正方体ABCD-A′B′C′D′的棱长为a , 连接A′C′,A′D , A′B , BD , BC′,C′D , 得到一个三棱锥.求:
19.(1)、某圆锥的侧面展开图为圆心角为 ,面积为 的扇形,求该圆锥的表面积和体积.(2)、已知直三棱柱 的底面是边长为 的正三角形,且该三棱柱的外接球的表面积为 ,求该三棱柱的体积.20. 如图,正方体ABCD-A′B′C′D′的棱长为a , 连接A′C′,A′D , A′B , BD , BC′,C′D , 得到一个三棱锥.求: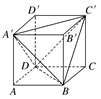 (1)、三棱锥A′-BC′D的表面积与正方体表面积的比值;(2)、三棱锥A′-BC′D的体积.
(1)、三棱锥A′-BC′D的表面积与正方体表面积的比值;(2)、三棱锥A′-BC′D的体积.