人教新课标A版 必修二 1.1空间几何体的结构
试卷更新日期:2020-07-31 类型:同步测试
一、单选题
-
1. 下列说法中正确的是( )A、棱柱的侧面可以是三角形 B、由6个大小一样的正方形所组成的图形是正方体的展开图 C、正方体的各条棱长都相等 D、棱柱的各条棱长都相等2. 下列说法中正确的是( )A、棱柱的面中,至少有两个面互相平行 B、棱柱中两个互相平行的平面一定是棱柱的底面 C、棱柱中一条侧棱就是棱柱的高 D、棱柱的侧面一定是平行四边形,但它的底面一定不是平行四边形3. 下列命题是真命题的是( )A、有两个侧面是矩形的四棱柱是直四棱柱 B、正四面体是特殊的正四棱锥 C、有一个面是多边形,其余各个面都是三角形的多面体叫做棱锥 D、正四棱柱是平行六面休4. 下列几何体中是棱柱的有( )
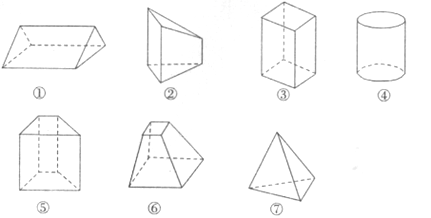 A、1个 B、2个 C、3个 D、4个5. 正方体被平面所截得的图形不可能是( )A、正三角形 B、正方形 C、正五边形 D、正六边形6. 下列几何体是组合体的是( )A、
A、1个 B、2个 C、3个 D、4个5. 正方体被平面所截得的图形不可能是( )A、正三角形 B、正方形 C、正五边形 D、正六边形6. 下列几何体是组合体的是( )A、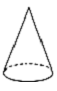 B、
B、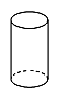 C、
C、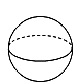 D、
D、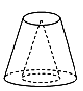 7. 如图所示,观察四个几何体,其中判断正确的是( ).
7. 如图所示,观察四个几何体,其中判断正确的是( ). A、⑴是棱台 B、⑵是圆台 C、⑶是棱锥 D、⑷不是棱柱8. 下图是由哪个平面图形旋转得到的( )
A、⑴是棱台 B、⑵是圆台 C、⑶是棱锥 D、⑷不是棱柱8. 下图是由哪个平面图形旋转得到的( )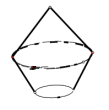 A、
A、 B、
B、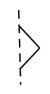 C、
C、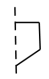 D、
D、 9. 某同学制作了一个对面图案均相同的正方形礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )
9. 某同学制作了一个对面图案均相同的正方形礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )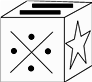 A、
A、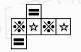 B、
B、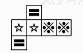 C、
C、 D、
D、 10. 一正四面体木块如图所示,点 是棱 的中点,过点P将木块锯开,使截面平行于棱 和 ,则下列关于截面的说法正确的是( ).
10. 一正四面体木块如图所示,点 是棱 的中点,过点P将木块锯开,使截面平行于棱 和 ,则下列关于截面的说法正确的是( ).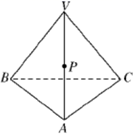 A、满足条件的截面不存在 B、截面是一个梯形 C、截面是一个菱形 D、截面是一个三角形11. 有一个长方形木块,三个侧面积分别为8,12,24,现将其削成一个正四面体模型,则该正四面体模型棱长的最大值为( )A、2 B、 C、4 D、12. 如图,棱长为l的正方体 中,P为线段 的中点, 分别为线段 和 棱 上任意一点,则 的最小值为( )
A、满足条件的截面不存在 B、截面是一个梯形 C、截面是一个菱形 D、截面是一个三角形11. 有一个长方形木块,三个侧面积分别为8,12,24,现将其削成一个正四面体模型,则该正四面体模型棱长的最大值为( )A、2 B、 C、4 D、12. 如图,棱长为l的正方体 中,P为线段 的中点, 分别为线段 和 棱 上任意一点,则 的最小值为( )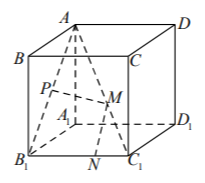 A、 B、 C、 D、2
A、 B、 C、 D、2二、多选题
-
13. 下列说法中不正确的是( )A、棱柱的侧面可以是三角形 B、正方体和长方体都是特殊的四棱柱 C、所有几何体的表面都能展开成平面图形 D、棱柱的各条棱都相等
三、填空题
-
14. 给出下列说法:
①圆柱的母线与它的轴可以不平行;
②圆锥的顶点、圆锥底面圆周上任意一点及底面圆的圆心三点的连线,都可以构成直角三角形;
③在圆台的上、下两底面圆周上各取一点,则这两点的连线是圆台的母线;
④圆柱的任意两条母线所在的直线是互相平行的.
其中正确的是(填序号).15. 如图,圆锥顶点为 ,底面圆心为 ,过轴 的截面 , 为 中点, , ,则从点 经圆锥侧面到点 的最短距离为.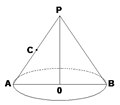 16. 一个直角三角形的三个顶点分别在底面棱长为2的正三棱柱的侧棱上,则该直角三角形斜边的最小值为
16. 一个直角三角形的三个顶点分别在底面棱长为2的正三棱柱的侧棱上,则该直角三角形斜边的最小值为
17. 有一个底面半径为 ,轴截面为正三角形的圆锥纸盒,在该纸盒内放一个棱长均为 的四面体,并且四面体在纸盒内可以任意转动,则 的最大值为.四、解答题
-
18. 如下图所示的图形绕虚线旋转一周后形成的几何体是由哪些简单几何体组成的?
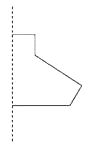 19. 如图所示,几何体可看作由什么图形旋转360°得到?画出平面图形和旋转轴.
19. 如图所示,几何体可看作由什么图形旋转360°得到?画出平面图形和旋转轴.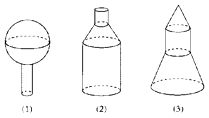 20. 正四面体所有棱长都为2,求它的高.21. 如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.
20. 正四面体所有棱长都为2,求它的高.21. 如图,在边长为2a的正方形ABCD中,E,F分别为AB,BC的中点,沿图中虚线将3个三角形折起,使点A,B,C重合,重合后记为点P.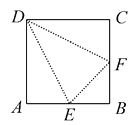
问:
(1)、折起后形成的几何体是什么几何体?(2)、这个几何体共有几个面,每个面的三角形有何特点?
(3)、每个面的三角形面积为多少?22. 如图,在正三棱柱ABC-A1B1C1中,AB=3,AA1=4,M为AA1的中点,P是BC上的一点,且由P沿棱柱侧面经过棱CC1到M的最短路线长为 ,设这条最短路线与CC1的交点为N.求: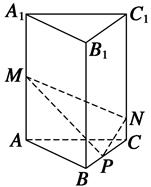 (1)、该三棱柱的侧面展开图的对角线的长;(2)、PC和NC的长.23. 如图,在长方体 中, ,P,Q分别为 与 中点.
(1)、该三棱柱的侧面展开图的对角线的长;(2)、PC和NC的长.23. 如图,在长方体 中, ,P,Q分别为 与 中点.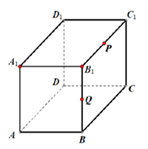
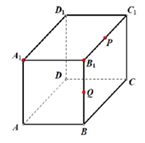

 (1)、经过P,Q作平面 ,平面 与长方体 六个表面所截的截面可能是n边形,请根据 的不同的取值分别作出截面图形形状(每种情况找一个代表类型,例如 只需要画一种,下面给了四幅图,可以不用完,如果不够请自行增加),保留作图痕迹;(2)、若R为直线 上的一点,且 ,求过 截面图形的周长.
(1)、经过P,Q作平面 ,平面 与长方体 六个表面所截的截面可能是n边形,请根据 的不同的取值分别作出截面图形形状(每种情况找一个代表类型,例如 只需要画一种,下面给了四幅图,可以不用完,如果不够请自行增加),保留作图痕迹;(2)、若R为直线 上的一点,且 ,求过 截面图形的周长.
-