新疆维吾尔自治区2020年数学中考二模试卷
试卷更新日期:2020-07-30 类型:中考模拟
一、选择题
-
1. 下列各数中,最小的数是( )A、0 B、-1 C、 D、12. 某几何体的展开图如图所示,则该几何体是( )
 A、三棱锥 B、四棱锥 C、三棱柱 D、四棱柱3. 如图,直线 与直线 相交,已知 ,则 的度数为( )
A、三棱锥 B、四棱锥 C、三棱柱 D、四棱柱3. 如图,直线 与直线 相交,已知 ,则 的度数为( )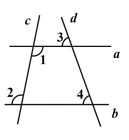 A、 B、 C、 D、4. 下列四个运算中,正确的个数是( )
A、 B、 C、 D、4. 下列四个运算中,正确的个数是( )① ;② ;③ ;④
A、1个 B、2个 C、3个 D、4个5. 某校学生会主席竞选中,参与投票的学生必须从进入决赛的四名选手中选1名,且只能选1名进行投票,根据投票结果,绘制了如下两幅不完整的统计图,则选手B的得票数为( )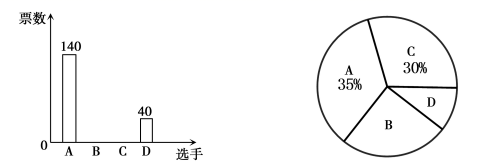 A、80 B、90 C、100 D、4006. 如图,在 中, 依据尺规作图的痕迹可判断 的度数是( )
A、80 B、90 C、100 D、4006. 如图,在 中, 依据尺规作图的痕迹可判断 的度数是( )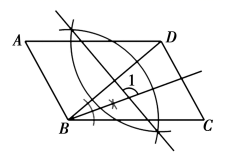 A、 B、 C、 D、7. 关于X的一元二次方程 有实数根,则K的取值范围在数轴上表示正确的是( )A、
A、 B、 C、 D、7. 关于X的一元二次方程 有实数根,则K的取值范围在数轴上表示正确的是( )A、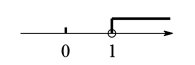 B、
B、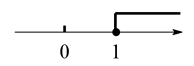 C、
C、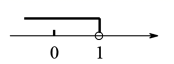 D、
D、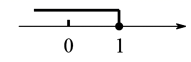 8. 如图,在长为62米、宽为42米的矩形草地上修同样宽的路,余下部分种植草坪,要使草坪的面积为2400平方米,设道路的宽为X米.则可列方程为( )
8. 如图,在长为62米、宽为42米的矩形草地上修同样宽的路,余下部分种植草坪,要使草坪的面积为2400平方米,设道路的宽为X米.则可列方程为( )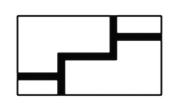 A、 B、 C、 D、9. 在矩形 中, 为 的中点,一块足够大的三角板的直角顶点与点G重合,将三角板绕点G旋转,三角板的两直角边分别交 或它们的延长线)于点 ,设 ,下列四个结论:① ;② ; ③ ;④ ,正确的个数是( )
A、 B、 C、 D、9. 在矩形 中, 为 的中点,一块足够大的三角板的直角顶点与点G重合,将三角板绕点G旋转,三角板的两直角边分别交 或它们的延长线)于点 ,设 ,下列四个结论:① ;② ; ③ ;④ ,正确的个数是( )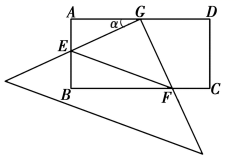 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
10. 使 有意义的x的取值范围是 .
11. 小华同学计算一组数据的方差时,写下的计算过程如下:,则其中的 .
12. 图中是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若最大的正方形E的边长为3则正方形 的面积之和为.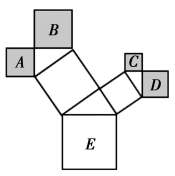 13. 如图, 是 的直径,弦 则阴影部分图形的面积为.
13. 如图, 是 的直径,弦 则阴影部分图形的面积为.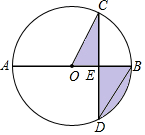 14. 观察下列等式: ,···试猜想 的个位数字是.15. 如图,二次函数 的图象经过点 ,对称轴为直线 下列 个结论: ; ; ; ; .其中正确的结论为. (注:只填写正确结论的序号)
14. 观察下列等式: ,···试猜想 的个位数字是.15. 如图,二次函数 的图象经过点 ,对称轴为直线 下列 个结论: ; ; ; ; .其中正确的结论为. (注:只填写正确结论的序号)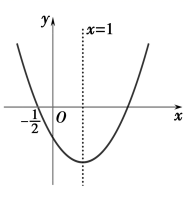
三、解答题
-
16. 计算: .17. 先化简,再求值: ,其中 .18. 如图,在矩形 中,过对角线 中点O的直线分别交边 于点 .
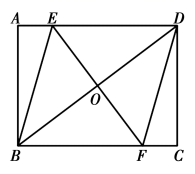 (1)、求证:四边形 是平行四边形;(2)、若 ,当四边形 是菱形时,求 的长.19. 如图,一次函数 的图象与反比例函数 在第一象限的图象交于 和B两点,与x轴交于点C,连接
(1)、求证:四边形 是平行四边形;(2)、若 ,当四边形 是菱形时,求 的长.19. 如图,一次函数 的图象与反比例函数 在第一象限的图象交于 和B两点,与x轴交于点C,连接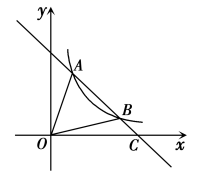 (1)、求反比例函数的解析式;(2)、若点P在x轴上,且 ,求点P的坐标.20. 一个智力挑战赛需要全部答对两道单项选择题,才能顺利通过第一关.第一道题有4个选项,第二道题有3个选项,这两道题小新都不会,不过小新还有一个“求助卡”没有用,使用“求助卡”可以让主持人去掉其中一题的一个错误选项.(1)、如果小新在第--题使用“求助卡”,请用树状图或者列表来分析小新顺利通过第一关的概率;(2)、从概率的角度分析,你建议小新在第几题使用“求助卡”.为什么.21. 如图,无人机在离地面40米的D处,测得楼房顶点C处俯角为 测得地面点B的俯角为 .已知点B到楼房 的距离为60米,求楼房AC的高度.(结果保留整数,参考数据: )
(1)、求反比例函数的解析式;(2)、若点P在x轴上,且 ,求点P的坐标.20. 一个智力挑战赛需要全部答对两道单项选择题,才能顺利通过第一关.第一道题有4个选项,第二道题有3个选项,这两道题小新都不会,不过小新还有一个“求助卡”没有用,使用“求助卡”可以让主持人去掉其中一题的一个错误选项.(1)、如果小新在第--题使用“求助卡”,请用树状图或者列表来分析小新顺利通过第一关的概率;(2)、从概率的角度分析,你建议小新在第几题使用“求助卡”.为什么.21. 如图,无人机在离地面40米的D处,测得楼房顶点C处俯角为 测得地面点B的俯角为 .已知点B到楼房 的距离为60米,求楼房AC的高度.(结果保留整数,参考数据: )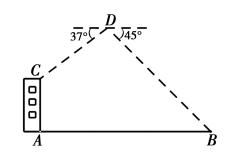 22. 我们知道,与三角形各边都相切的圆叫做三角形的内切圆,则三角形可以称为圆的外切三角形.如图1, 与 的三边 分别相切于点 则 叫做 的外切三角形.以此类推,各边都和圆相切的四边形称为圆外切四边形.如图2, 与四边形ABCD的边 分别相切于点 则四边形 叫做 的外切四边形.
22. 我们知道,与三角形各边都相切的圆叫做三角形的内切圆,则三角形可以称为圆的外切三角形.如图1, 与 的三边 分别相切于点 则 叫做 的外切三角形.以此类推,各边都和圆相切的四边形称为圆外切四边形.如图2, 与四边形ABCD的边 分别相切于点 则四边形 叫做 的外切四边形.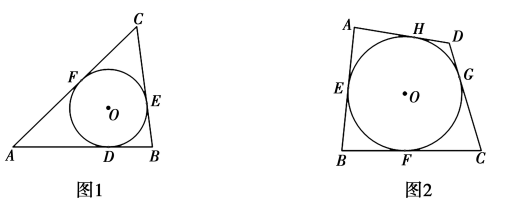 (1)、如图2,试探究圆外切四边形 的两组对边 与 之间的数量关系,猜想: (横线上填“>”,“<”或“=”);(2)、利用图2证明你的猜想(写出已知,求证,证明过程);(3)、用文字叙述上面证明的结论:;(4)、若圆外切四边形的周长为 相邻的三条边的比为 ,求此四边形各边的长.23. 如图,已知抛物线 与x轴交于 两点,交y轴于点 对称轴是直线 .
(1)、如图2,试探究圆外切四边形 的两组对边 与 之间的数量关系,猜想: (横线上填“>”,“<”或“=”);(2)、利用图2证明你的猜想(写出已知,求证,证明过程);(3)、用文字叙述上面证明的结论:;(4)、若圆外切四边形的周长为 相邻的三条边的比为 ,求此四边形各边的长.23. 如图,已知抛物线 与x轴交于 两点,交y轴于点 对称轴是直线 .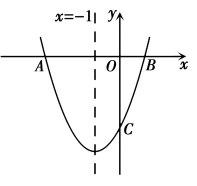 (1)、求抛物线的解析式及点C的坐标;(2)、连接 是线段 上一点,点E关于直线 的对称点F正好落在 上,求点F的坐标;(3)、动点M从点 出发,以每秒2个单位长度的速度向点A运动,到达点A即停止运动.过点M作x轴的垂线交抛物线于点N交线段 于点Q.设运动时间为 秒.
(1)、求抛物线的解析式及点C的坐标;(2)、连接 是线段 上一点,点E关于直线 的对称点F正好落在 上,求点F的坐标;(3)、动点M从点 出发,以每秒2个单位长度的速度向点A运动,到达点A即停止运动.过点M作x轴的垂线交抛物线于点N交线段 于点Q.设运动时间为 秒.①连接 ,若 与 相似,请直接写出t的值;
② 能否为等腰三角形.若能,求出t的值;若不能,请说明理由.