新疆昌吉市2020年数学中考一模试卷
试卷更新日期:2020-07-30 类型:中考模拟
一、选择题
-
1. 的相反数是( )A、-2 B、2 C、 D、2. 某个几何体的三视图如图所示,该几何体是( )
 A、
A、 B、
B、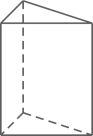 C、
C、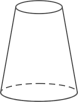 D、
D、 3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,AB//CD,∠AEG=126°,GE平分∠CGF,则∠BFG的度数等于( )
3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,AB//CD,∠AEG=126°,GE平分∠CGF,则∠BFG的度数等于( )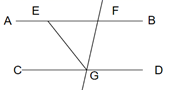 A、108° B、126° C、128° D、72°5. 某中学九(1)班参加了“勿忘12.9---激昂青春我拥有”的合唱比赛,共有7位评委打分,求得其平均数、中位数、众数、方差.若去掉最高分与最低分后,一定不会发生改变的是( )A、中位数 B、平均数 C、众数 D、方差6. 已知关于x的一元二次方程 有两个实数根,则实数m的取值范围是( )A、 B、 C、m<2且 D、 且7. 国家实施“精准扶贫”政策以来,很多贫困人口走向了致富的道路,某地区2017年底有贫困人口10万人,通过社会各界的努力,2019年底贫困人口减少至1万人.设2017年底至2019年底该地区贫困人口的年平均下降率为x,根据题意列方程得( )A、10(1-2x)=1 B、10(1-x)2=1 C、10(1+2x)=1 D、10(1+x)2=18. 如图,将边长为8㎝的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN , 则线段CN的长是( )
A、108° B、126° C、128° D、72°5. 某中学九(1)班参加了“勿忘12.9---激昂青春我拥有”的合唱比赛,共有7位评委打分,求得其平均数、中位数、众数、方差.若去掉最高分与最低分后,一定不会发生改变的是( )A、中位数 B、平均数 C、众数 D、方差6. 已知关于x的一元二次方程 有两个实数根,则实数m的取值范围是( )A、 B、 C、m<2且 D、 且7. 国家实施“精准扶贫”政策以来,很多贫困人口走向了致富的道路,某地区2017年底有贫困人口10万人,通过社会各界的努力,2019年底贫困人口减少至1万人.设2017年底至2019年底该地区贫困人口的年平均下降率为x,根据题意列方程得( )A、10(1-2x)=1 B、10(1-x)2=1 C、10(1+2x)=1 D、10(1+x)2=18. 如图,将边长为8㎝的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN , 则线段CN的长是( )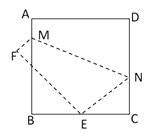 A、3cm B、4cm C、5cm D、6cm9. 已知:二次函数y = ax2+ bx + c (a≠0)的图象如图所示,下列结论中:
A、3cm B、4cm C、5cm D、6cm9. 已知:二次函数y = ax2+ bx + c (a≠0)的图象如图所示,下列结论中:①abc>0;②2a + b>0;③a +b<m(am +b)(m≠1);④(a+c)2< b2;⑤a >1.其中正确的项是( )
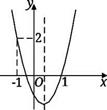 A、①②⑤ B、①③④ C、①②④ D、②④⑤
A、①②⑤ B、①③④ C、①②④ D、②④⑤二、填空题
-
10. 将20 200 000用科学记数法表示为。11. 如果代数式 有意义,则x的取值范围.12. 在同一副扑克牌中抽取2张“梅花”,3张“方块”,1张“黑桃”.将这6张牌背面朝上,从中任意抽取1张,是“梅花”的概率为.13. 如图,AB是圆O的直径,CD⊥AB于点E,交圆O于点D,OF⊥AC于点F,BD=5,则OF=.
 14. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2020的坐标为.
14. 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么点A2020的坐标为. 15. 如图,直线 与双曲线 交于A、B两点,连接OA、OB, 轴于点M, 轴于点N,有以下结论:① ;② ;③ 则 ;④当 时, .其中结论正确的是
15. 如图,直线 与双曲线 交于A、B两点,连接OA、OB, 轴于点M, 轴于点N,有以下结论:① ;② ;③ 则 ;④当 时, .其中结论正确的是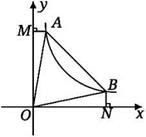
三、解答题
-
16. 计算:17. 先化简,再求值. ,从 中选一个适合的整数代入求值.18. 某社区招募了40位居民参加“众志成城,抗击疫情”志愿者服务活动,对志愿者一天的服务时长进行调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
频数分布表
组别
时间/小时
频数/人数
A组
0≤ <1
2
B组
1≤ <2
m
C组
2≤ <3
10
D组
3≤ <4
12
E组
4≤ <5
7
F组
≥5
4
扇形统计图

请根据图表中的信息解答下列问题:
(1)、求频数分布表中的m的值;(2)、求B组,C组在扇形统计图中分别对应扇形的圆心角的度数,并补全扇形统计图;(3)、已知F组的志愿者中,只有1名女志愿者.要从该组中选取两名志愿者分发生活物资,请用树状图或列表的方法求2名志愿者恰好都是男士的概率.19. 如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E、F.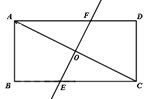 (1)、求证:四边形AECF是菱形;(2)、当BE=3,AF=5时,求AC的长.20. 如图,某同学参加社会实践活动,站在甲、乙两栋楼中间,看甲楼顶部A的仰角为60°,看乙楼顶部C的仰角为45°,已知乙楼的高度为41.5米,该同学的的身高为1.5米.求甲楼AB的高度.(结果保留根号)
(1)、求证:四边形AECF是菱形;(2)、当BE=3,AF=5时,求AC的长.20. 如图,某同学参加社会实践活动,站在甲、乙两栋楼中间,看甲楼顶部A的仰角为60°,看乙楼顶部C的仰角为45°,已知乙楼的高度为41.5米,该同学的的身高为1.5米.求甲楼AB的高度.(结果保留根号)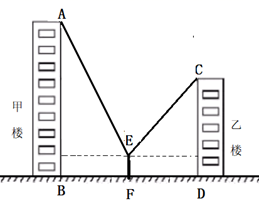 21. 如图1所示,在A,B两地之间有汽车站C站,货车由A地驶往B地,客车由B地驶往C站.两车同时出发,匀速行驶.图2是货车、客车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.
21. 如图1所示,在A,B两地之间有汽车站C站,货车由A地驶往B地,客车由B地驶往C站.两车同时出发,匀速行驶.图2是货车、客车离C站的路程y1 , y2(千米)与行驶时间x(小时)之间的函数关系图象.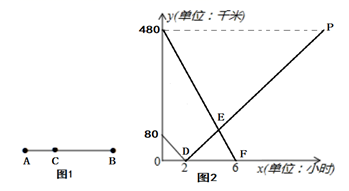 (1)、填空:A,B两地相距千米;(2)、求两小时后,货车离C站的路程y1与行驶时间x之间的函数关系式;(3)、客、货两车何时相遇?22. 如图,在△ABC中,∠A=90°,以AB为直径的ʘO交BC于D,点E为AC的中点,连接DE.
(1)、填空:A,B两地相距千米;(2)、求两小时后,货车离C站的路程y1与行驶时间x之间的函数关系式;(3)、客、货两车何时相遇?22. 如图,在△ABC中,∠A=90°,以AB为直径的ʘO交BC于D,点E为AC的中点,连接DE.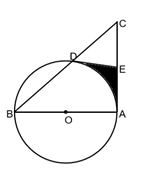 (1)、求证:DE是ʘO的切线;(2)、若∠BAD=50°,AC=6,CD=4,求图中阴影部分的面积.23. 如图,在平面直角坐标系中,抛物线 与x轴交于点A,B(1,0),与y轴交于点C(0,3),对称轴为直线l.
(1)、求证:DE是ʘO的切线;(2)、若∠BAD=50°,AC=6,CD=4,求图中阴影部分的面积.23. 如图,在平面直角坐标系中,抛物线 与x轴交于点A,B(1,0),与y轴交于点C(0,3),对称轴为直线l.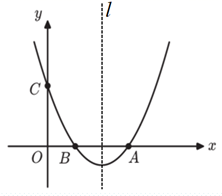 (1)、求抛物线的解析式及点A的坐标;(2)、在对称轴l上是否存在一点M,使得△BCM周长最小?若存在,求出△BCM周长;若不存在,请说明理由;(3)、若点P是抛物线上一动点,从点C沿抛物线向点A运动,过点P作PD// 轴,交AC于点D,当△ADP是直角三角形时,求点P的坐标.
(1)、求抛物线的解析式及点A的坐标;(2)、在对称轴l上是否存在一点M,使得△BCM周长最小?若存在,求出△BCM周长;若不存在,请说明理由;(3)、若点P是抛物线上一动点,从点C沿抛物线向点A运动,过点P作PD// 轴,交AC于点D,当△ADP是直角三角形时,求点P的坐标.