新疆昌吉市2020年数学中考四模试卷
试卷更新日期:2020-07-30 类型:中考模拟
一、选择题
-
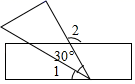
1. -2的相反数是( )A、2 B、-2 C、 D、2. 自然界中的数学不胜枚举,如蜜蜂建造的蜂房既坚固又省料,其厚度为0.0073厘米,将0.0073用科学记数法表示为( )A、 B、 C、 D、3. 如图,将一块含有 的直角三角板的顶点放在直尺的一边上,若 ,那么 的度数是
 A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 为了解学生课外阅读时间情况,随机收集了30名学生一天课外阅读时间,整理如下表:
A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 为了解学生课外阅读时间情况,随机收集了30名学生一天课外阅读时间,整理如下表:阅读时间/小时
0.5及以下
0.7
0.9
1.1
1.3
1.5及以上
人数
2
9
6
5
4
4
则本次调查中阅读时间的中位数和众数分别是( )
A、0.7和0.7 B、0.9和0.7 C、1和0.7 D、0.9和1.16. 若关于x的一元二次方程 有两个实数根,则k的取值范围是( )A、 B、 C、 D、7. 如图,在△ABC中,点D , E分别在AB , AC上,DE∥BC , AD=CE . 若AB:AC=3:2,BC=10,则DE的长为( )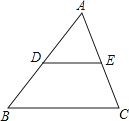 A、3 B、4 C、5 D、68. 如图,在矩形ABCD中,点F在AD上,点E在BC上,把矩形沿EF折叠后,使点D恰好落 在BC边上的G点处,若矩形面积为 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
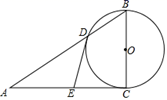
A、3 B、4 C、5 D、68. 如图,在矩形ABCD中,点F在AD上,点E在BC上,把矩形沿EF折叠后,使点D恰好落 在BC边上的G点处,若矩形面积为 且∠AFG=60°,GE=2BG,则折痕EF的长为( ) A、1 B、 C、2 D、9. 如图,四边形 内接于半圆O, 为直径, ,过点D作 于点E,连接 交 于点F.若 , ,则 的长为( )
A、1 B、 C、2 D、9. 如图,四边形 内接于半圆O, 为直径, ,过点D作 于点E,连接 交 于点F.若 , ,则 的长为( )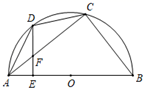 A、8 B、10 C、15 D、24
A、8 B、10 C、15 D、24二、填空题
-
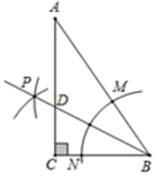
10. 分解因式: =11. 分式方程 的解为.12. 圆锥的侧面展开图是一个弧长为6π的扇形,则这个圆锥底面半径是.13. 如图,在Rt△ABC中,∠C=90°,以顶点B为圆心,适当长度为半径画弧,分别交AB,BC于点M,N,再分别以点M,N为圆心,大于 的长为半径画弧,两弧交于点P,作射线BP交AC于点D.若∠A=30°,则 .
 14. 如图,Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y= (x>0)与y= (x<0)的图象上,则tan∠BAO的值为 .
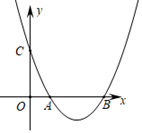
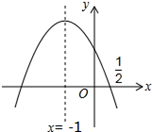
14. 如图,Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y= (x>0)与y= (x<0)的图象上,则tan∠BAO的值为 .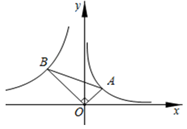 15. 如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点 ,有下列结论:
15. 如图,抛物线y=ax2+bx+c的对称轴是x=﹣1.且过点 ,有下列结论:①abc 0; ②a﹣2b+4c=0; ③25a﹣10b+4c=0; ④3b+2c 0; ⑤a﹣b≥m(am﹣b);
其中所有正确的结论是.(填写正确结论的序号)
三、解答题
-
16. 计算:17. 先化简,再求值: ,其中x的值从不等式组 的整数解中选取.18. 现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
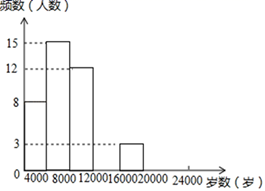
步数
频数
频率
0≤x<4000
8
a
4000≤x<8000
15
0.3
8000≤x<12000
12
b
12000≤x<16000
c
0.2
16000≤x<20000
3
0.06
20000≤x<24000
d
0.04
请根据以上信息,解答下列问题:
(1)、写出a,b,c,d的值并补全频数分布直方图;(2)、本市约有37600名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?(3)、若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步)的两名教师与大家分享心得,求被选取的两名教师恰好不在同一组的概率.19. 如图,在正方形 中,点 是 的中点,连接 ,过点 作 交 于点 ,交 于点 .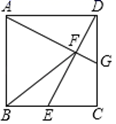 (1)、证明:G是 中点;(2)、连接 ,证明: .20. 图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂AC=44cm,灯罩CD=32cm,灯臂与底座构成的∠CAB=60°.CD可以绕点C上下调节一定的角度.使用发现:当CD与水平线所成的角为30°时,台灯光线最佳.现测得点D到桌面的距离为54.06cm.请通过计算说明此时台灯光线是否为最佳?(参考数据: 取1.73).
(1)、证明:G是 中点;(2)、连接 ,证明: .20. 图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂AC=44cm,灯罩CD=32cm,灯臂与底座构成的∠CAB=60°.CD可以绕点C上下调节一定的角度.使用发现:当CD与水平线所成的角为30°时,台灯光线最佳.现测得点D到桌面的距离为54.06cm.请通过计算说明此时台灯光线是否为最佳?(参考数据: 取1.73).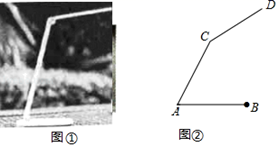 21. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量 (件 与销售价 (元/件)之间的函数关系如图所示.
21. 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量 (件 与销售价 (元/件)之间的函数关系如图所示.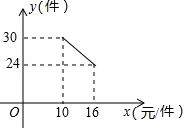 (1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求每天的销售利润W(元 与销售价 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?
(1)、求 与 之间的函数关系式,并写出自变量 的取值范围;(2)、求每天的销售利润W(元 与销售价 (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?