新疆昌吉市2020年数学中考二模试卷
试卷更新日期:2020-07-30 类型:中考模拟
一、选择题
-
1. 2020的相反数是( )A、 2020 B、﹣2020 C、 D、2. 某个几何体的三视图如图所示,该几何体是( )
 A、
A、 B、
B、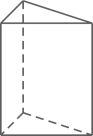 C、
C、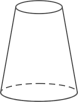 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是 , , , ,则射击成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁5. 如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=60°,则∠2=( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是 , , , ,则射击成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁5. 如图,AB∥CD,EF⊥AB于E,EF交CD于F,已知∠1=60°,则∠2=( )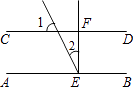 A、20° B、60° C、30° D、45°6.
A、20° B、60° C、30° D、45°6.下图是统计一位病人的体温变化图,则这位病人在16时的体温约是( )
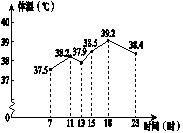 A、37.8℃ B、38℃ C、38.7℃ D、39.1℃7. 关于 的方程 的两根互为相反数,则 的值为( )A、±2 B、2 C、-2 D、不能确定8. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所用的时间与原计划生产450台机器所用的时间相同.若设原计划平均每天生产x台机器,则可列方程为( )A、 = B、 = C、 = D、 =9. 如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=( )
A、37.8℃ B、38℃ C、38.7℃ D、39.1℃7. 关于 的方程 的两根互为相反数,则 的值为( )A、±2 B、2 C、-2 D、不能确定8. 某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所用的时间与原计划生产450台机器所用的时间相同.若设原计划平均每天生产x台机器,则可列方程为( )A、 = B、 = C、 = D、 =9. 如图,正方形ABCD中,E为AB上一点,AF⊥DE于点F,已知DF=5EF=5,过C、D、F的⊙O与边AD交于点G,则DG=( )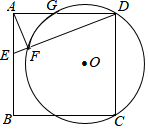 A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
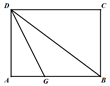
10. 2019年12月以来,新冠病毒席卷全球.截止2020年5月14日,全球累计确诊约435万例,用科学记数法表示全球确诊约为例.11. 计算 =12. 若正多边形的内角和是540°,则该正多边形的一个外角为 .13. 在10个外观相同的产品中,有8个合格产品,现从中任意抽取1个进行检测,抽到不合格产品的概率是.14. 如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,再折叠使AD边与BD重合,得折痕DG,若AB=8,BC=6,则AG的长为 .
 15. 如图所示,反比例函数 在第一象限内分支上有一动点A,连接AO并延长与另一分支交于点B,以AB为边作一个等边△ABC,使得点C落在第四象限内.在点A运动过程中,直接写出△ABC面积的最小值.
15. 如图所示,反比例函数 在第一象限内分支上有一动点A,连接AO并延长与另一分支交于点B,以AB为边作一个等边△ABC,使得点C落在第四象限内.在点A运动过程中,直接写出△ABC面积的最小值.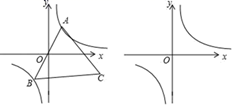
三、解答题
-
16. 计算: 3tan30°﹣(1﹣π)0+|1 |.17. 解不等式组: ,并把它的解集在数轴上表示出来18. 如图所示,在矩形ABCD中,O是AC与BD的交点,过点O的直线EF与AB,CD的延长线分别交于点E,F.
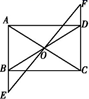 (1)、求证:△BOE≌△DOF;(2)、当EF与AC满足什么条件时,四边形AECF是菱形?并证明你的结论.19. 如图,一艘船由A港沿北偏东65°方向航行 km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.
(1)、求证:△BOE≌△DOF;(2)、当EF与AC满足什么条件时,四边形AECF是菱形?并证明你的结论.19. 如图,一艘船由A港沿北偏东65°方向航行 km至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向.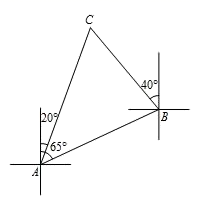
求:
(1)、∠C的度数;(2)、A,C两港之间的距离为多少km.20. 某校380名学生参加了这学期的“读书伴我行”活动要求每人在这学期读书4~7本活动结束后随机抽查了20名学生每人的读书量,并分为四种等级,A:4本;B:5本;C:6本;D:7本.将各等级的人数绘制成尚不完整的扇形图(如图1)和条形图(如图2)
回答下列问题:
(1)、这20名学生每人这学期读书量的众数是 ▲ 本,中位数是 ▲ 本;补全条形图(2)、估计380名学生在这学期共读书多少本;(3)、若A等级的四名学生中有男生、女生各两名现从中随机选出两名学生写读书感想,请用画树状图的方法求出刚好选中一名男生、一名女生的概率.21. 货车和轿车分别从甲、乙两地同时出发,沿同一公路相向而行.轿车出发2.4h后休息,直至与货车相遇后,以原速度继续行驶.设货车出发xh后,货车、轿车分别到达离甲地y1km和y2km的地方,图中的线段OA、折线BCDE分别表示y1、y2与x之间的函数关系.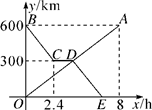 (1)、求点D的坐标,并解释点D的实际意义;(2)、求线段DE所在直线的函数表达式;(3)、当货车出发h时,两车相距200km.22. 如图,AB是⊙O的直径,点C在半圆上,点D在圆外,DE⊥AB于点E交AC于点F,且DF=CD
(1)、求点D的坐标,并解释点D的实际意义;(2)、求线段DE所在直线的函数表达式;(3)、当货车出发h时,两车相距200km.22. 如图,AB是⊙O的直径,点C在半圆上,点D在圆外,DE⊥AB于点E交AC于点F,且DF=CD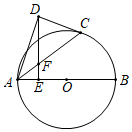 (1)、求证:CD是⊙O的切线;(2)、若点F是AC的中点,DF=2EF=2 ,求⊙O半径.23. 如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点(A点在B点左侧),A(﹣1, 0),B(3,0),直线l与抛物线交于A,C两点,其中C点的横坐标为2.
(1)、求证:CD是⊙O的切线;(2)、若点F是AC的中点,DF=2EF=2 ,求⊙O半径.23. 如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点(A点在B点左侧),A(﹣1, 0),B(3,0),直线l与抛物线交于A,C两点,其中C点的横坐标为2.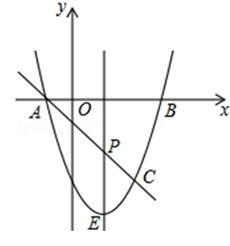 (1)、求抛物线的函数解析式;(2)、P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)、点G是抛物线上的动点,在x轴上是否存在点F,使A,C,F,G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
(1)、求抛物线的函数解析式;(2)、P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;(3)、点G是抛物线上的动点,在x轴上是否存在点F,使A,C,F,G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.