陕西省西安市曲江一中2020年数学中考一模试卷
试卷更新日期:2020-07-30 类型:中考模拟
一、选择题
-
1. ﹣2020的绝对值是( )A、﹣2020 B、2020 C、﹣ D、2. 如果有一个正方体,它的展开图可能是下列四个展开图中的
 A、
A、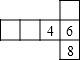 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 设正比例函数y=mx的图象经过点A(m , 4),且y的值随x值的增大而减小,则m=( )A、2 B、-2 C、4 D、-45. 如图,将三角板的直角顶点放在直尺的一边 上.若∠1=65°,则∠2 的度数为( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 设正比例函数y=mx的图象经过点A(m , 4),且y的值随x值的增大而减小,则m=( )A、2 B、-2 C、4 D、-45. 如图,将三角板的直角顶点放在直尺的一边 上.若∠1=65°,则∠2 的度数为( )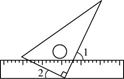 A、15° B、35° C、25° D、40°6. 在平面直角坐标系中,将直线y=3x的图象向左平移m个单位,使其与直线y=﹣x+6的交点在第二象限,则m的取值范围是( )A、m>2 B、m<2 C、m>6 D、m<67. 如图,已知四边形ABCD中,AC平分∠BAD,AB=AC=5,AD=3,BC=CD.则点C到AB的距离是( )
A、15° B、35° C、25° D、40°6. 在平面直角坐标系中,将直线y=3x的图象向左平移m个单位,使其与直线y=﹣x+6的交点在第二象限,则m的取值范围是( )A、m>2 B、m<2 C、m>6 D、m<67. 如图,已知四边形ABCD中,AC平分∠BAD,AB=AC=5,AD=3,BC=CD.则点C到AB的距离是( )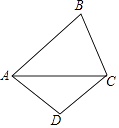 A、 B、 C、3 D、28. 如图,矩形 中, , , 于 ,则 ( )
A、 B、 C、3 D、28. 如图,矩形 中, , , 于 ,则 ( )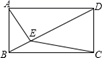 A、 B、 C、 D、9. 如图,△ABC内接于⊙O,AC=5,BC=12,且∠A=90°+∠B,则点O到AB的距离为( )
A、 B、 C、 D、9. 如图,△ABC内接于⊙O,AC=5,BC=12,且∠A=90°+∠B,则点O到AB的距离为( )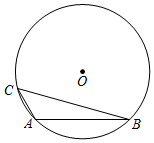 A、 B、 C、 D、410. 二次函数y=x2+bx+c的图象经过坐标原点O和点A(7,0),直线AB交y轴于点B(0,﹣7),动点C(x,y)在直线AB上,且1<x<7,过点C作x轴的垂线交抛物线于点D,则CD的最值情况是( )A、有最小值9 B、有最大值9 C、有最小值8 D、有最大值8
A、 B、 C、 D、410. 二次函数y=x2+bx+c的图象经过坐标原点O和点A(7,0),直线AB交y轴于点B(0,﹣7),动点C(x,y)在直线AB上,且1<x<7,过点C作x轴的垂线交抛物线于点D,则CD的最值情况是( )A、有最小值9 B、有最大值9 C、有最小值8 D、有最大值8二、填空题
-
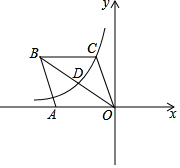
11. 将实数0,﹣ ,2.7,﹣1.4,0.14用“<”号连接起来应为.12. 任意五边形的内角和与外角和的差为度.13. 如图,在平面直角坐标系中,菱形OABC的边OA在x轴的负半轴上,反比例函数y= (x<0)的图象经过对角线OB的中点D和顶点C.若菱形OABC的面积为6,则k的值等于 .
 14. 如图,线段BC和动点A构成△ABC,∠BAC=120°,BC=3,则△ABC周长的最大值.
14. 如图,线段BC和动点A构成△ABC,∠BAC=120°,BC=3,则△ABC周长的最大值.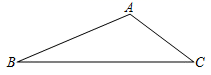
三、解答题
-
15. 计算:16. 先化简,再求值:(x+1)÷(2+ ),其中x=﹣ .17. 如右图,已知点P是线段MN外一点,请利用直尺和圆规画一点Q,使得点Q到M、N两点的距离相等,且点Q与点M、P在同一条直线上.(保留作图痕迹)
 18. 如图,AB∥CF,D,E分别是AB,AC上的点,DE=EF.求证:△ADE≌△CFE.
18. 如图,AB∥CF,D,E分别是AB,AC上的点,DE=EF.求证:△ADE≌△CFE.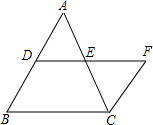 19. 某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.
19. 某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查,将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.等级
频数
频率
优秀
20
良好
合格
10
不合格
5

请根据以上信息,解答下列问题:
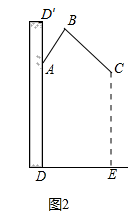
(1)、本次调查随机抽取了名学生;表中 , ;(2)、补全条形统计图;(3)、若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.20. 图1是一种淋浴喷头,图2是图1的示意图,若用支架把喷头固定在点A处,手柄长 , AB与墙壁 的夹角 ,喷出的水流BC与AB形成的夹角 ,现在住户要求:当人站在E处淋浴时,水流正好喷洒在人体的C处,且使 问:安装师傅应将支架固定在离地面多高的位置?(参考数据: ).

 21. 甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分别表示甲、乙两人与A地的距离y甲、y乙与他们所行时间x(h)之间的函数关系.
21. 甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分别表示甲、乙两人与A地的距离y甲、y乙与他们所行时间x(h)之间的函数关系.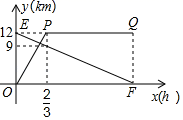 (1)、求线段OP对应的y甲与x的函数关系式并注明自变量x的取值范围;(2)、求y乙与x的函数关系式以及乙到达A地所用的时间;(3)、经过小时,甲、乙两人相距2km.22. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.23. 已知在Rt△ABC中,∠C=90°;以斜边AB上的一点O为圆心作圆O,与AC、BC分别相切与点D、E.
(1)、求线段OP对应的y甲与x的函数关系式并注明自变量x的取值范围;(2)、求y乙与x的函数关系式以及乙到达A地所用的时间;(3)、经过小时,甲、乙两人相距2km.22. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.23. 已知在Rt△ABC中,∠C=90°;以斜边AB上的一点O为圆心作圆O,与AC、BC分别相切与点D、E.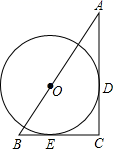 (1)、求证:CD=CE;(2)、若AC=8,AB=10;求AD的长.24. 已知二次函数L与y轴交于点C(0,3),且过点(1,0),(3,0).(1)、求二次函数L的解析式及顶点H的坐标(2)、已知x轴上的某点M(t,0);若抛物线L关于点M对称的新抛物线为L′,且点C、H的对应点分别为C′,H′;试说明四边形CHC′H′为平行四边形.(3)、若平行四边形的边与某一条对角线互相垂直时,称这种平行四边形为“和谐四边形”;在(2)的条件下,当平行四边形CHC′H′为“和谐四边形”时,求t的值.25.
(1)、求证:CD=CE;(2)、若AC=8,AB=10;求AD的长.24. 已知二次函数L与y轴交于点C(0,3),且过点(1,0),(3,0).(1)、求二次函数L的解析式及顶点H的坐标(2)、已知x轴上的某点M(t,0);若抛物线L关于点M对称的新抛物线为L′,且点C、H的对应点分别为C′,H′;试说明四边形CHC′H′为平行四边形.(3)、若平行四边形的边与某一条对角线互相垂直时,称这种平行四边形为“和谐四边形”;在(2)的条件下,当平行四边形CHC′H′为“和谐四边形”时,求t的值.25.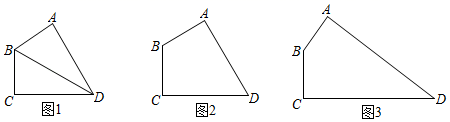 (1)、问题提出:
(1)、问题提出:如图1,在四边形ABCD中,AB=BC,AD=CD=3,∠BAD=∠BCD=90°,∠ADC=60°,则四边形ABCD的面积为;
(2)、问题探究:如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠ABC=135°,AB=2 ,BC=3,在AD、CD上分别找一点E、F,使得△BEF的周长最小,并求出△BEF的最小周长;
(3)、问题解决:如图3,在四边形ABCD中,AB=BC=2,CD=10,∠ABC=150°,∠BCD=90°,则在四边形ABCD中(包含其边沿)是否存在一点E,使得∠AEC=30°,且使四边形ABCE的面积最大.若存在,找出点E的位置,并求出四边形ABCE的最大面积;若不存在,请说明理由.