辽宁省大连2020年数学中考模拟试卷（4月）

试卷更新日期：2020-07-30 类型：中考模拟

进入出卷网下载

一、选择题

1. 如图所示，a和b的大小关系是（）

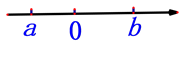A、a＞b B、a＜b C、2a=b D、2b=a

查看试题解析
2. (a，﹣6)关于x轴对称的点的坐标为（）

A、(﹣a，6) B、(a，6) C、(a，﹣6) D、(﹣a，﹣6)

查看试题解析
3. 下列运算不正确的是（）

A、a²•a³＝a⁵ B、（y³）⁴＝y¹² C、（﹣2x）³＝﹣8x³ D、x³+x³＝2x⁶

查看试题解析
4. 下列立体图形中，左视图是三角形的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，菱形ABCD的对角线AC ， BD相交于点O ，过点A作AH⊥BC于点H ，连接OH ，若OB＝4，S_菱形ABCD＝24，则OH的长为（）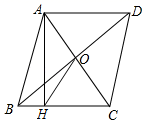

A、3 B、4 C、5 D、6

查看试题解析
6. 用2、3、4三个数字排成一个三位数，则排出的数是偶数的概率为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{3}{5}$ D、 $\frac{2}{3}$

查看试题解析
7. 如图，将直尺与含30°角的三角尺摆放在一起，若∠1=20°，则∠2的度数是（）

A、30° B、40° C、50° D、60°

查看试题解析
8. 我国古代《四元玉鉴》中记载“二果问价”问题，其内容如下：九百九十九文钱，甜果苦果买一千，甜果九个十一文，苦果七个四文钱，试问甜苦果几个，又问各该几个钱？若设买甜果x个，买苦果y个，则下列关于x、y的二元一次方程组中符合题意的是（）

A、 ${\begin{matrix} x + y = 999 \\ \frac{11}{9} x + \frac{4}{7} y = 1000 \end{matrix}$ B、 ${\begin{matrix} x + y = 1000 \\ \frac{9}{11} x + \frac{7}{4} y = 999 \end{matrix}$ C、 ${\begin{matrix} x + y = 1000 \\ 99 x + 28 y = 999 \end{matrix}$ D、 ${\begin{matrix} x + y = 1000 \\ \frac{11}{9} x + \frac{4}{7} y = 999 \end{matrix}$

查看试题解析
9. 某班15名同学为灾区捐款，他们捐款数额统计如下：

捐款数额（元）

5

10

20

50

100

人数（名）

2

4

5

3

1

下列说法正确的是（）.

A、众数是100 B、平均数是20 C、中位数是20 D、极差是20

查看试题解析
10. 如图，矩形OABC的边OA在x轴上，OA＝8，OC＝4，把△ABC沿直线AC折叠，得到△ADC，CD交x轴于点E，则点E的坐标是（）

A、（4，0） B、（3，0） C、（0，3） D、（5，0）

查看试题解析

二、填空题

11. 分解因式6xy²－9x²y－y³ = .

查看试题解析
12. 移动互联网已经全面进入人们的日常生活.截止2018年12月，全国4G用户总数947000 000，这个数用科学记数法表示为.

查看试题解析
13. 用10米长的铝材制成一个矩形窗框，使它的面积为6平方米.若设它的一条边长为x 米，则根据题意可列出关于x的方程为.

查看试题解析
14. 如图，圆锥的底面半径OB＝6cm，高OC＝8cm，则该圆锥的侧面积是cm² ．

查看试题解析
15. 如图，两块三角尺的直角顶点靠在一起，BC=3，EF=2，G 为 DE 上一动点，把三角尺DEF 绕直角顶点 F 旋转一周，在这个旋转过程中，B，G 两点的最小距离为.

查看试题解析
16. 如图，小明为了测量校园里旗杆AB的高度，将测角仪CD竖直放在距旗杆底部B点6m的位置，在D处测得旗杆顶端A的仰角为53°，若测角仪的高度是1.5m，则旗杆AB的高度约为m．（精确到0.1m．参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）

查看试题解析

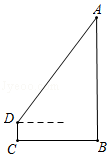
三、解答题

17. 计算：

(1)、（ $\sqrt{20}$ + $\sqrt{5}$ + 5）÷ $\sqrt{5}$ － $\sqrt{\frac{1}{3}}$ × $\sqrt{24}$ － $\sqrt{5}$ ；

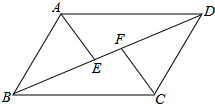
(2)、（－3）^﹣²+ $\sqrt{8}$ －|1－2 $\sqrt{2}$ |－（ $\sqrt{6}$ －3）⁰

查看试题解析
18. 解一元一次不等式组： ${\begin{matrix} - 5 x + 3 > 3 (x - 2) \\ \frac{x + 1}{2} \leq 1 - \frac{5 - x}{6} \end{matrix}$

查看试题解析
19. 如图，在平行四边形ABCD中，E，F分别是对角线BD上的两点，且BE＝DF.求证：AE＝CF.

查看试题解析
20. 时代中学从学生兴趣出发，实施体育活动课走班制.为了了解学生最喜欢的一种球类运动，以便合理安排活动场地，在全校至少喜欢一种球类（乒乓球、羽毛球、排球、篮球、足球）运动的1200名学生中，随机抽取了若干名学生进行调查（每人只能在这五种球类运动中选择一种）.调查结果统计如下：
球类名称
乒乓球
羽毛球
排球
篮球
足球
人数
42
$a$
15
33
$b$

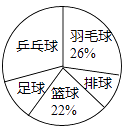
解答下列问题：

(1)、这次抽样调查中的样本是；

(2)、统计表中， $a =$ ， $b =$ ；

(3)、试估计上述1200名学生中最喜欢乒乓球运动的人数.

查看试题解析
21. 甲、乙两公司为“2019东台西溪·国际半程马拉松比赛”各制作6400个相同的纪念牌，已知甲公司的人数比乙公司人数少20%，乙公司比甲公司人均少做20个，甲、乙两公司各有多少人？

查看试题解析
22. 如图，一次函数y₁=kx+b的图象与反比例函数 $y_{2} = \frac{m}{x}$ 的图象交于点A（﹣2，﹣5），C（5，n），交y轴于点B，交x轴于点D.

(1)、求反比例函数 $y_{2} = \frac{m}{x}$ 和一次函数y₁=kx+b的表达式；

(2)、连接OA，OC，求△AOC的面积；

(3)、根据图象，直接写出y₁＞y₂时x的取值范围.

查看试题解析
23. 已知：如图，BE是△ABC的外接圆O的直径，CD是△ABC的高.

(1)、求证：AC·BC＝BE·CD；

(2)、已知CD＝6、AD＝3、BD＝8，求⊙O的直径BE的长.

查看试题解析
24. 在长方形ABCD中，AB＝3，BC＝4，动点P从点A开始按A→B→C→D的方向运动到点D.如图，设动点P所经过的路程为x，△APD的面积为y.(当点P与点A或D重合时，y＝0)

(1)、写出y与x之间的函数表达式；

(2)、画出此函数的图象.

查看试题解析
25. 如图，在△ABC中，∠ACB＝90°，∠ABC＝30°，△CDE是等边三角形，点D在边AB上.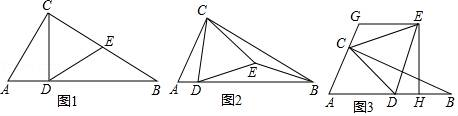

(1)、如图1，当点E在边BC上时，求证DE＝EB；

(2)、如图2，当点E在△ABC内部时，猜想ED和EB数量关系，并加以证明；

(3)、如图3，当点E在△ABC外部时，EH⊥AB于点H，过点E作GE∥AB，交线段AC的延长线于点G，AG＝5CG，BH＝3.求CG的长.

查看试题解析
26. 如图，点A，B，C都在抛物线y＝ax²﹣2amx+am²﹣9（其中a＞0）上，AB∥x轴，点P是抛物线的顶点，tan∠PBA＝2，∠BAC＝45°.

(1)、填空：抛物线的顶点P的坐标为（用含m的代数式表示）；

(2)、求△ABC的面积（用含a的代数式表示）；

(3)、若△ABC的面积为10，当2m﹣3≤x≤2m+5时，y的最小值为5，求m的值.

查看试题解析

球类名称	乒乓球	羽毛球	排球	篮球	足球
人数	42	$a$	15	33	$b$

捐款数额（元）	5	10	20	50	100
人数（名）	2	4	5	3	1