辽宁省鞍山市立山区2020年数学中考二模试卷
试卷更新日期:2020-07-30 类型:中考模拟
一、选择题
-
1. 下列图形中是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 是方程 的两根, 的值是( )A、2017 B、2018 C、2019 D、20203. 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
2. 是方程 的两根, 的值是( )A、2017 B、2018 C、2019 D、20203. 如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )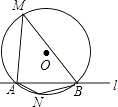 A、2 B、4 C、4 D、84. 如图,已知,第一象限内的点 在反比例函数 的图象上,第四象限内的点 在反比例函数 的图象上.且 , ,则 的值为( )
A、2 B、4 C、4 D、84. 如图,已知,第一象限内的点 在反比例函数 的图象上,第四象限内的点 在反比例函数 的图象上.且 , ,则 的值为( )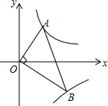 A、 B、6 C、 D、-65. 如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是( )
A、 B、6 C、 D、-65. 如图,在一个由4×4个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积比是( )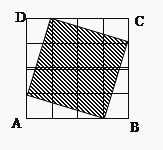 A、3 :4 B、5 :8 C、9 :16 D、1 :26. 已知二次函数y=ax2+bx+c的图像经过点(0,m)、(4、m)、(1,n),若n<m,则( )A、a>0且4a+b=0 B、a<0且4a+b=0 C、a>0且2a+b=0 D、a<0且2a+b=07. 如图,半径为1的⊙O与正五边形ABCDE相切于点A、C,则劣弧AC的长度为( )
A、3 :4 B、5 :8 C、9 :16 D、1 :26. 已知二次函数y=ax2+bx+c的图像经过点(0,m)、(4、m)、(1,n),若n<m,则( )A、a>0且4a+b=0 B、a<0且4a+b=0 C、a>0且2a+b=0 D、a<0且2a+b=07. 如图,半径为1的⊙O与正五边形ABCDE相切于点A、C,则劣弧AC的长度为( ) A、 π B、 π C、 π D、 π8. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )
A、 π B、 π C、 π D、 π8. 如图,正方形 的边长为 ,动点 , 同时从点 出发,在正方形的边上,分别按 , 的方向,都以 的速度运动,到达点 运动终止,连接 ,设运动时间为 , 的面积为 ,则下列图象中能大致表示 与 的函数关系的是( )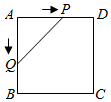 A、
A、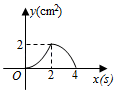 B、
B、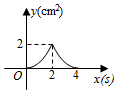 C、
C、 D、
D、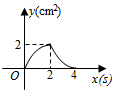
二、填空题
-
9. 如图,在网格中,小正方形的边长均为1,点 在格点上,则 的正切值是.
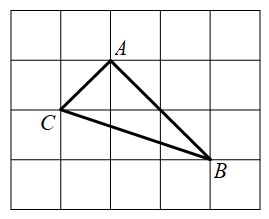 10. 如图,直线 交 轴于点 ,交 轴于点 ,点 是 轴上一动点,以点 为圆心,以1个单位长度为半径作 ,当 与直线 相切时,点 的坐标是 .
10. 如图,直线 交 轴于点 ,交 轴于点 ,点 是 轴上一动点,以点 为圆心,以1个单位长度为半径作 ,当 与直线 相切时,点 的坐标是 . 11. 如图,反比例函数 在第一象限内的图象,直线AB//x轴,并分别交两条曲线A、B两点,若S△AOB=2,则k2-k1的值为 .
11. 如图,反比例函数 在第一象限内的图象,直线AB//x轴,并分别交两条曲线A、B两点,若S△AOB=2,则k2-k1的值为 .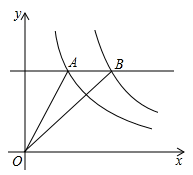 12. 若二次函数 的顶点在x轴上,则 .13. 抛物线 的对称轴为直线 .若关于x的一元二次方程 在 的范围内有实数根,则t的取值范围是.14. 如图,直线 与抛物线 交于 , 两点,点 是 轴上的一个动点,当 的周长最小时, .
12. 若二次函数 的顶点在x轴上,则 .13. 抛物线 的对称轴为直线 .若关于x的一元二次方程 在 的范围内有实数根,则t的取值范围是.14. 如图,直线 与抛物线 交于 , 两点,点 是 轴上的一个动点,当 的周长最小时, .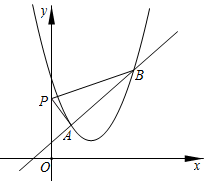 15. 在同一平面直角坐标系中,若抛物线 与 关于 轴对称,则符合条件的 ; .16. 如图,过点 作y轴的垂线交直线 于点 ,过点 作直线L的垂线,交y轴于点 ,过点 作y轴的垂线交直线L于点 …,这样依次下去,得到 ,…,其面积分别记为 ,…,则 为.
15. 在同一平面直角坐标系中,若抛物线 与 关于 轴对称,则符合条件的 ; .16. 如图,过点 作y轴的垂线交直线 于点 ,过点 作直线L的垂线,交y轴于点 ,过点 作y轴的垂线交直线L于点 …,这样依次下去,得到 ,…,其面积分别记为 ,…,则 为.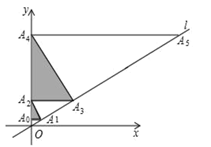
三、解答题
-
17. 计算:18. 双曲线 (k为常数,且 )与直线 交于 两点.
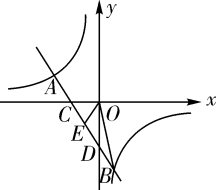 (1)、求k与b的值;(2)、如图,直线AB交x轴于点C,交y轴于点D,若点E为CD的中点,求△BOE的面积.19. 某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月末累计进馆608人次,若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳能力不超过500人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由.20. 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)、求k与b的值;(2)、如图,直线AB交x轴于点C,交y轴于点D,若点E为CD的中点,求△BOE的面积.19. 某校为响应我市全民阅读活动,利用节假日面向社会开放学校图书馆据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月末累计进馆608人次,若进馆人次的月平均增长率相同.(1)、求进馆人次的月平均增长率;(2)、因条件限制,学校图书馆每月接纳能力不超过500人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接纳第四个月的进馆人次,并说明理由.20. 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,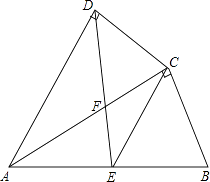 (1)、求证:AC2=AB•AD;(2)、求证:CE∥AD;(3)、若AD=4,AB=6,求 的值.21. 某公司展销如图所示的长方形工艺品,该工艺品长60 ,宽40 ,中间镶有宽度相同的三条丝绸花边.
(1)、求证:AC2=AB•AD;(2)、求证:CE∥AD;(3)、若AD=4,AB=6,求 的值.21. 某公司展销如图所示的长方形工艺品,该工艺品长60 ,宽40 ,中间镶有宽度相同的三条丝绸花边.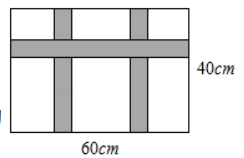 (1)、若丝绸花边的面积(阴影面积)为650 ,求丝绸花边的宽度;(2)、已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天还需支付各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件,那么该公司应该把销售单价定为多少元,才能使每天所获销售利润最大,最大利润是多少.22. 如图,在一场马拉松比赛中,某人在大楼 处,测得起点拱门 的顶部 的俯角为 ,底部 的俯角为 ,如果 处离地面的高度 米,求起点拱门 的高度,(结果精确到; ,参考数据: )
(1)、若丝绸花边的面积(阴影面积)为650 ,求丝绸花边的宽度;(2)、已知该工艺品的成本是40元/件,如果以单价100元/件销售,那么每天可售出200件,另每天还需支付各种费用2000元,根据销售经验,如果将销售单价降低1元,每天可多售出20件,同时,为了完成销售任务,该公司每天至少要销售800件,那么该公司应该把销售单价定为多少元,才能使每天所获销售利润最大,最大利润是多少.22. 如图,在一场马拉松比赛中,某人在大楼 处,测得起点拱门 的顶部 的俯角为 ,底部 的俯角为 ,如果 处离地面的高度 米,求起点拱门 的高度,(结果精确到; ,参考数据: )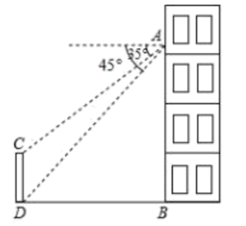 23. 如图, 为⊙ 的直径,点 在 的延长线上,点 在⊙ 上,且 .
23. 如图, 为⊙ 的直径,点 在 的延长线上,点 在⊙ 上,且 . (1)、求证: 是⊙ 的切线;(2)、已知 , ,点 是 的中点, ,垂足为 , 交 于点 ,求 的长.24. 一连锁店销售某品牌商品,该商品的进价是60元.因为是新店开业,所以连锁店决定当月前10天进行试营业活动,活动期间该商品的售价为每件80元,据调查研究发现:当天销售件数 (件)和时间第x(天)的关系式为 ( ),已知第4天销售件数是40件,第6天销售件数是44件.活动结束后,连锁店重新制定该商品的销售价格为每件100元,每天销售的件数也发生变化:当天销售数量 (件)与时间第x(天)的关系为: ( ).(1)、求 关于x的函数关系式;
(1)、求证: 是⊙ 的切线;(2)、已知 , ,点 是 的中点, ,垂足为 , 交 于点 ,求 的长.24. 一连锁店销售某品牌商品,该商品的进价是60元.因为是新店开业,所以连锁店决定当月前10天进行试营业活动,活动期间该商品的售价为每件80元,据调查研究发现:当天销售件数 (件)和时间第x(天)的关系式为 ( ),已知第4天销售件数是40件,第6天销售件数是44件.活动结束后,连锁店重新制定该商品的销售价格为每件100元,每天销售的件数也发生变化:当天销售数量 (件)与时间第x(天)的关系为: ( ).(1)、求 关于x的函数关系式;
(2)、若某天的日毛利润是1120元,求x的值;(3)、因为该连锁店是新店开业,所以试营业结束后,厂家给这个连锁店相应的优惠政策:当这个连锁店日销售量达到60件后(不含60),每多销售1件产品,当日销售的所有商品进价减少2元,设该店日销售量超过60件的毛利润总额为W,请直接写出W关于x的函数解析式,及自变量x的取值范围: .
25. 如图1,在 中, , ,点 分别是 的中点,连接 .(1)、探索发现: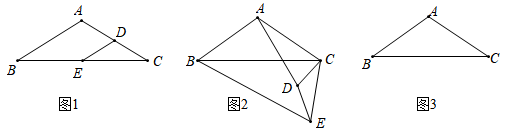
图1中, 的值为; 的值为;
(2)、拓展探究若将 绕点 逆时针方向旋转一周,在旋转过程中 的大小有无变化,请仅就图2的情形给出证明;
(3)、问题解决当 旋转至 三点在同一直线时,直接写出线段 的长.
26. 如图,抛物线 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为 .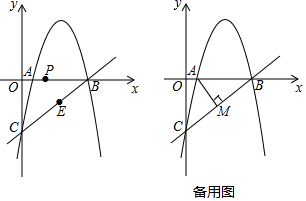 (1)、求抛物线的解析式.(2)、点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.(3)、过点A作 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
(1)、求抛物线的解析式.(2)、点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.(3)、过点A作 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.