江苏省南京市2020年数学中考模拟试卷（5月）

试卷更新日期：2020-07-30 类型：中考模拟

进入出卷网下载

一、选择题

1. 2019年“五一”假期期间，我市共接待国内、外游客6.632万人次，实现旅游综合收入502亿元，则“旅游综合收入”用科学记数法表示正确的是（）

A、 5.02×10²元 B、5.02×10⁶元 C、5.02×10⁸元 D、5.02×10¹⁰元

查看试题解析
2. 计算（﹣1.5）²⁰¹⁸×（ $\frac{2}{3}$ ）²⁰¹⁹的结果是（）

A、﹣ $\frac{3}{2}$ B、 $\frac{3}{2}$ C、﹣ $\frac{2}{3}$ D、 $\frac{2}{3}$

查看试题解析
3. 把不等式 $2 - x$ ＜1的解集在数轴上表示正确的是（）

A、 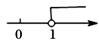B、 C、 D、

查看试题解析
4. 从不同方向看某物体得到如图所示的三个图形，那么该物体是（）

A、长方体 B、圆锥 C、正方体 D、圆柱

查看试题解析
5. 小军家距学校5千米，原来他骑自行车上学，学校为保障学生安全，新购进校车接送学生，若校车速度是他骑车速度的2倍，现在小军乘校车上学可以从家晚10分钟出发，结果与原来到校时间相同.设小军骑车的速度为x千米/小时，则所列方程正确的为（）

A、 $\frac{5}{x}$ + $\frac{1}{6}$ ＝ $\frac{5}{2 x}$ B、 $\frac{5}{x}$ ﹣ $\frac{1}{6}$ ＝ $\frac{5}{2 x}$ C、 $\frac{5}{x}$ +10＝ $\frac{5}{2 x}$ D、 $\frac{5}{x}$ ﹣10＝ $\frac{5}{2 x}$

查看试题解析
6. 如图在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B₁、C₁处，点B₁在x轴上，再将△AB₁C₁绕点B₁顺时针旋转到△A₁B₁C₂的位置，点C₂在x轴上，将△A₁B₁C₂绕点C₂顺时针旋转到△A₂B₂C₂的位置，点A₂在x轴上，依次进行下去…若点A（ $\frac{3}{2}$ ，0），B（0，2），则点B₂₀₁₈的坐标为（）

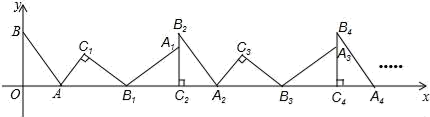A、（6048，0） B、（6054，0） C、（6048，2） D、（6054，2）

查看试题解析

二、填空题

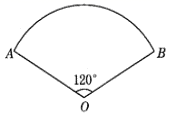
7. 若二次根式 $\sqrt{2 x - 1}$ 有意义，则x的取值范围是．

查看试题解析
8. 分式 $\frac{3 - x}{2 - x}$ 的值比分式 $\frac{1}{x - 2}$ 的值大3，则x为.

查看试题解析
9. 分解因式6xy²－9x²y－y³ = .

查看试题解析
10. 计算： $\sqrt{7}$ × $\sqrt{14}$ =.

查看试题解析
11. 已知x₁ ， x₂是关于的一元二次方程x²﹣3x+a＝0的两个实数根，x₁²﹣3x₁x₂+x₂²＝4，则a＝.

查看试题解析
12. 如图，用一个圆心角为120°的扇形围成一个无底的圆锥，如果这个圆锥底面圆的半径为 $3 c m$ ，则这个扇形的半径是 $c m$ .

查看试题解析
13. 如图，点A在双曲线y＝ $\frac{k}{x}$ 上，AB⊥x轴于点B，若△ABO的面积是3，则k＝.

查看试题解析
14. 如图所示，平行四边形内有两个全等的正六边形，若阴影部分的面积记为 $S_{1}$ ，平行四边形的面积记为 $S_{2}$ ，则 $\frac{S_{1}}{S_{2}}$ 的值为.

查看试题解析
15. 如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE.若∠D＝70°，则∠EAC的度数为.

查看试题解析
16. 在△ABC中，AB＝2 $\sqrt{3}$ ，BC＝a，∠C＝60°，如果对于a的每一个确定的值，都存在两个不全等的△ABC，那么a的取值范围是.

查看试题解析

三、解答题

17.

(1)、计算 ${(\sqrt{3})}^{- 1} + {(π - \sqrt{2})}^{0} - tan 30^{\circ}$

(2)、化简： $(a - 2) (a + 3) - {(a - 1)}^{2}$

查看试题解析
18. 先化简，再求值： $(\frac{2 x}{2 x + 1} - \frac{1}{4 x^{2} + 2 x}) \div (1 - \frac{4 x^{2} + 1}{4 x}) ，$ 其中 $x = 3.$

查看试题解析

19. 某市教育主管部门为了解学生的作业量情况，随机抽取了几所中学八年级的部分学生进行了一次调查，并根据收集到的信息进行了统计，绘制了下面两幅尚不完整的统计图.请你根据统计图、表中所提供的信息解答下列问题：

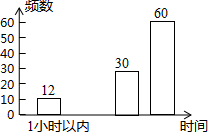(1)、本次共抽取了名学生进行调查；

(2)、x＝ ▲ ， y＝ ▲ ，补全条形统计图；

(3)、若这几所中学八年级的学生共有3200人，请估计做作业时间在2小时以上的学生人数是多少？

(4)、由图表可知，这次被调查的八年级学生的作业时间的中位数一定落在1.5小时﹣2小时这一时段内，你认为这种判断正确吗？（不需要说明理由）

写作业时间	频数	频率
1小时以内	12	0.1
1﹣1.5	x	0.15
1.5﹣2	30	0.25
2小时以上	60	y

查看试题解析

20. 如图，四边形ABCD是平行四边形，BE∥DF，且分别交对角线AC于点E，F，连接ED，BF，求证：△ABE≌△CDF.

查看试题解析
21. “元旦大酬宾!”，某商场设计的促销活动如下：在一个不透明的箱子里放有3张相同的卡片，卡片上分别标有“10元”、“20元”和“30元”的字样，规定：在本商场同一日内，顾客每消费满300元，就可以在箱子里摸出一张卡片，记下钱数后放回，再从中摸出一张卡片.商场根据两张卡片所标金额的和返还相等价格的购物券，购物券可以在本商场消费.某顾客刚好消费300元.

(1)、该顾客最多可得到元购物券；

(2)、请你用画树状图或列表的方法，求出该顾客所获得购物券的金额不低于40元的概率.

查看试题解析
22. 学校与图书馆在同一条笔直道路上，甲从学校去图书馆，乙从图书馆回学校，甲、乙两人都匀速步行且同时出发，乙先到达目的地.两人之间的距离y（米）与时间t（分钟）之间的函数关系如图所示.

(1)、根据图象信息，当t＝分钟时甲乙两人相遇，甲的速度为米/分钟，乙的速度为米/分钟；

(2)、图中点A的坐标为；

(3)、求线段AB所直线的函数表达式；

(4)、在整个过程中，何时两人相距400米？

查看试题解析
23. 某校九年级数学兴趣小组的同学进行社会实践活动时，想利用所学的解直角三角形的知识测量某塔的高度.他们先在点D用高1.5米的测角仪 $D A$ 测得塔顶M的仰角为30°，然后沿 $D F$ 方向前行 $40 m$ 到达点E处，在E处测得塔顶M的仰角为60°.请根据他们的测量数据求此塔 $M F$ 的高.（结果精确 $0.1 m$ ，参考数据： $\sqrt{2} = 1.41$ ， $\sqrt{3} = 1.73$ ， $\sqrt{6} = 2.45$ ).

查看试题解析
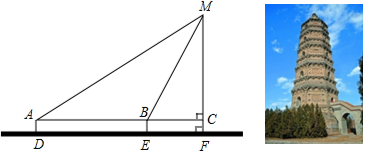24. 已知Rt△AEC中，∠E＝90°，请按如下要求进行操作和判断：

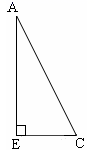(1)、尺规作图：作△AEC的外接圆⊙O，并标出圆心O（不写画法）；

(2)、延长CE，在CE的延长线上取点B，使EB＝EC，连结AB，设AB与⊙O的交点为D（标出字母B、D），判断：图中 $\overset{⌢}{D E}$ 与 $\overset{⌢}{E C}$ 相等吗？请说明理由.

查看试题解析
25. 已知：二次函数C₁：y₁＝ax²+2ax+a-1（a≠0）.

(1)、把二次函数C₁的表达式化成y＝a（x-h）²+b（a≠0）的形式，并写出顶点坐标；

(2)、已知二次函数C₁的图象经过点A(-3，1).
①a的值；

②点B在二次函数C₁的图象上，点A，B关于对称轴对称，连接AB.二次函数C₂：y₂＝kx²+kx（k≠0）的图象，与线段AB只有一个交点，则k的取值范围.

查看试题解析
26. 如图，AB为⊙O的直径，AE是⊙O的弦，C是弧AE的中点，弦CG⊥AB于点D，交AE于点F，过点C作⊙O的切线，交BA延长线于点P，连接BE

(1)、求证：PC∥AE；

(2)、若sin∠P＝ $\frac{3}{5}$ ，CF＝5，求BE的长.

查看试题解析
27. 如图①，在△ABC中，∠C＝90°，AC＝15，BC＝20，经过点C的⊙O与△ABC的每条边都相交.⊙O与AC边的另一个公共点为D，与BC边的另一个公共点为E，与AB边的两个公共点分别为F、G.设⊙O的半径为r.

(1)、（操作感知）
根据题意，仅用圆规在图①中作出一个满足条件的⊙O，并标明相关字母；

(2)、（初步探究）
求证：CD²+CE²＝4r²；

(3)、当r＝8时，则CD²+CE²+FG²的最大值为；

(4)、（深入研究）
直接写出满足题意的r的取值范围；对于范围内每一个确定的r的值，CD²+CE²+FG²都有最大值，每一个最大值对应的圆心O所形成的路径长为.

查看试题解析