江苏省溧阳市2020年数学中考一模试卷
试卷更新日期:2020-07-30 类型:中考模拟
一、选择题
-
1. -3的相反数是( )A、 B、 C、3 D、-32. 已知刚上市的水蜜桃每千克12元,则 千克水蜜桃共多少元?( )A、m-12 B、m+12 C、 D、12m3. 下列图形中,哪一个是四棱锥的侧面展开图?( )A、
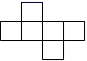 B、
B、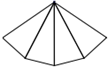 C、
C、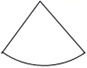 D、
D、 4. 一个正比例函数的图象经过(2,-1),则它的表达式为 )A、y=-2x B、y=2x C、 D、5. 下列命题中,假命题是( )A、两组对边平行的四边形是平行四边形 B、三个角是直角的四边形是矩形 C、四条边相等的四边形是菱形 D、有一个角是直角的平行四边形是正方形6. 已知 为整数,且 < < ,则 等于( )A、1 B、2 C、3 D、47. 为了全面保障学校艺术节表演的整体效果,王老师在操场中标记了几个关键位置,如图是利用平面直角坐标系画出的关键位置分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示点A的坐标为(-1,-2),表示点B的坐标为(1,1),则表示其他位置的点的坐标正确的是( )
4. 一个正比例函数的图象经过(2,-1),则它的表达式为 )A、y=-2x B、y=2x C、 D、5. 下列命题中,假命题是( )A、两组对边平行的四边形是平行四边形 B、三个角是直角的四边形是矩形 C、四条边相等的四边形是菱形 D、有一个角是直角的平行四边形是正方形6. 已知 为整数,且 < < ,则 等于( )A、1 B、2 C、3 D、47. 为了全面保障学校艺术节表演的整体效果,王老师在操场中标记了几个关键位置,如图是利用平面直角坐标系画出的关键位置分布图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示点A的坐标为(-1,-2),表示点B的坐标为(1,1),则表示其他位置的点的坐标正确的是( ) A、C(-1,0) B、D(-3,1) C、E(-7,-3) D、F(2,-3)8. 如图,在平面直角坐标系中,△AOB中,∠AOB=90°,∠ABO=30°,顶点A在反比例函y= (x>0)上运动,此时顶点B也在反比例函数y= 上运动,则m的值为( )
A、C(-1,0) B、D(-3,1) C、E(-7,-3) D、F(2,-3)8. 如图,在平面直角坐标系中,△AOB中,∠AOB=90°,∠ABO=30°,顶点A在反比例函y= (x>0)上运动,此时顶点B也在反比例函数y= 上运动,则m的值为( )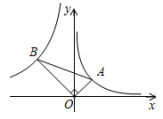 A、-9 B、-12 C、-15 D、-18
A、-9 B、-12 C、-15 D、-18二、填空题
-
9. 计算:|-2|-1= .10. 计算:x(x-2) =.11. 分解因式:2a²-4a+2=.12. 点P(-2,3),则点P关于x轴对称的点的坐标是.13. 地球与火星的距离大约为5500万公里,用科学记数法表示这个距离为万公里.14. 如图,正方形二维码的边长为2cm,为了测算图中黑色部分的面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.75左右,据此可估计黑色部分的面积的为cm2.
 15. 如图,直线l1∥l2∥l3 , 等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=.
15. 如图,直线l1∥l2∥l3 , 等边△ABC的顶点B、C分别在直线l2、l3上,若边BC与直线l3的夹角∠1=25°,则边AB与直线l1的夹角∠2=. 16. 如图,△ABC是⊙O的内接三角形,∠BAC=60°, 的长是 ,则⊙O的半径是.
16. 如图,△ABC是⊙O的内接三角形,∠BAC=60°, 的长是 ,则⊙O的半径是.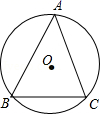 17. 在△ABC中,AC=5,AB=6,则△ABC面积的最大值为.18. 如图,在⊙O中,点A、点B在⊙O上,∠AOB=90°,OA=6,点C在OA上,且OC=2AC,点D是OB的中点,点M是劣弧AB上的动点,则CM+2DM的最小值为.
17. 在△ABC中,AC=5,AB=6,则△ABC面积的最大值为.18. 如图,在⊙O中,点A、点B在⊙O上,∠AOB=90°,OA=6,点C在OA上,且OC=2AC,点D是OB的中点,点M是劣弧AB上的动点,则CM+2DM的最小值为.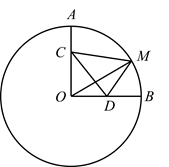
三、解答题
-
19. 计算: -(1- )0+4tan45°.20. 解方程组和不等式组:(1)、(2)、21. 如图,将Rt△ABC沿BC所在直线平移得到△DEF.
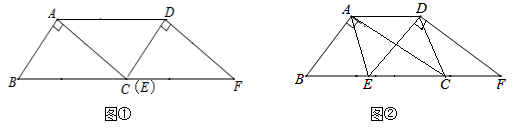 (1)、如图①,当点E移动到点C处时,连接AD,求证:△CDA≌△ABC;(2)、如图②,当点E移动到BC中点时,连接AD、AE、CD,请你判断四边形AECD的形状,并说明理由.22. 某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取
(1)、如图①,当点E移动到点C处时,连接AD,求证:△CDA≌△ABC;(2)、如图②,当点E移动到BC中点时,连接AD、AE、CD,请你判断四边形AECD的形状,并说明理由.22. 某校决定加强羽毛球、篮球、乒乓球、排球、足球五项球类运动,每位同学必须且只能选择一项球类运动,对该校学生随机抽取 进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图:
进行调查,根据调查结果绘制了如下不完整的频数分布表和扇形统计图: 运动项目
频数(人数)
羽毛球
30
篮球

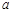
乒乓球
36
排球
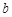
足球
12

请根据以上图表信息解答下列问题:
(1)、频数分布表中的a= , b=;(2)、在扇形统计图中,“排球”所在的扇形的圆心角为 度;(3)、全校有多少名学生选择参加乒乓球运动?23. 疫情过后,为了促进消费,某商场设计了一种促销活动:在一个不透明的箱子里放有四个相同的小球,球上分别标有“10元”、“20元”、“30元”和“40元”的字样,规定:在本商场同一日内,顾客每消费满500元,就可以在箱子里先后摸出两个球(第一次摸出后不放回)。商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费500元.(1)、该顺客最多可得到元购物券;(2)、请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于60元的概率.24. 疫情期间,甲、乙两个口罩工厂共同承担口罩生产任务,甲工厂单独完成此项任务比乙工厂单独完成此项任务需多用10天,且甲工厂单独生产45天和乙工厂单独生产30天的工作量相同.(1)、甲、乙两工厂单独完成此项任务需要多少天?(2)、若甲、乙两工厂共同生产了3天后,乙工厂因设备检修停止生产,由甲工厂维续生产,为了不影响任务进度,甲工厂的工作效率提高到原来的2倍,要使甲工厂总的工作量不少于乙工厂总的工作量的2倍,那么甲工厂需要至少再单独生产多少天?25. 京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).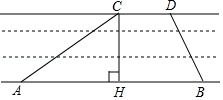 26. 在平面直角坐标系xOy中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作d(M).(1)、已知点E(0,4),
26. 在平面直角坐标系xOy中,正方形ABCD的顶点分别为A(0,1),B(-1,0),C(0,-1),D(1,0).对于图形M,给出如下定义:P为图形M上任意一点,Q为正方形ABCD边上任意一点,如果P,Q两点间的距离有最大值,那么称这个最大值为图形M的“正方距”,记作d(M).(1)、已知点E(0,4),①直接写出d(点E)的值;
②直线y=kx+4(k≠0)与x轴交于点F,当d(线段EF)取最小值时,求k的取值范围;
(2)、⊙T的圆心为T(7,t),半径为1.若d(⊙T)<11,请直接写出t的取值范围.27. 如图,在平面直角坐标系中,矩形OABC的顶点O是坐标原点,OA、OC分别在x轴、y轴的正半轴上,且OA=5,OC=4. (1)、如图①,将矩形沿对角线OB折叠,使得点A落在点D处,OD与CB相交于点E,请问重叠部分△OBE是什么三角形?说明你的理由:并求出这个三角形的面积;(2)、如图②,点E、F分别是OC、OA边上的点,将△OEF沿EF折叠,使得点O正好落在BC边上的D点,过点D作DH⊥OA,交EF于点G,交OA于点H,若CD=2,求点G的坐标;(3)、如图③,照(2)中条件,当点E、F在OC、OA上移动时,点D也在边BC上随之移动,请直接写出BD的取值范围.28. 如图,抛物线的图像经过点A(4,4),B(5,0)和原点O,点P为抛物线上的一个动点,过点P作x轴的垂线,垂足为D(m,0)(m>0),并与直线OA交于点C.
(1)、如图①,将矩形沿对角线OB折叠,使得点A落在点D处,OD与CB相交于点E,请问重叠部分△OBE是什么三角形?说明你的理由:并求出这个三角形的面积;(2)、如图②,点E、F分别是OC、OA边上的点,将△OEF沿EF折叠,使得点O正好落在BC边上的D点,过点D作DH⊥OA,交EF于点G,交OA于点H,若CD=2,求点G的坐标;(3)、如图③,照(2)中条件,当点E、F在OC、OA上移动时,点D也在边BC上随之移动,请直接写出BD的取值范围.28. 如图,抛物线的图像经过点A(4,4),B(5,0)和原点O,点P为抛物线上的一个动点,过点P作x轴的垂线,垂足为D(m,0)(m>0),并与直线OA交于点C.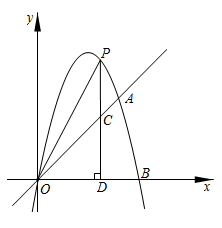 (1)、求出抛物线的函数表达式;(2)、连接OP,当S△OPC= S△OCD时,求出此时的点P坐标;(3)、在直线OA上取一点M,使得以P、C、M为顶点的三角形与△OCD全等,求出点M的坐标.
(1)、求出抛物线的函数表达式;(2)、连接OP,当S△OPC= S△OCD时,求出此时的点P坐标;(3)、在直线OA上取一点M,使得以P、C、M为顶点的三角形与△OCD全等,求出点M的坐标.