江苏省江阴市华士片2020年数学中考模拟试卷（6月）

试卷更新日期：2020-07-30 类型：中考模拟

进入出卷网下载

一、选择题

1. 2的倒数是（）。

A、2 B、 $\frac{1}{2}$ C、 $- \frac{1}{2}$ D、-2

查看试题解析
2. 下列计算结果是x⁵的为（）

A、x²•x³ B、x⁶－x C、x¹⁰÷x² D、(x³)²

查看试题解析
3. 下面图形分别表示低碳、节水、节能和绿色食品四个标志，其中的轴对称图形是（）

A、 B、 C、 D、

查看试题解析
4. 一组数据：2，3，6，4，3，5，这组数据的中位数、众数分别是（）

A、3，3 B、3，4 C、3.5，3 D、5，3

查看试题解析
5. 函数 $y = \frac{x}{2 - x}$ 中自变量x的取值范围是（）

A、x≠2 B、 $x > 0$ C、 $x \leq 2$ D、 $x \leq 2$ 且x≠0

查看试题解析
6. 如图，从⊙O外一点A引圆的切线AB，切点为B，连接AO并延长交圆于点C，连接BC.若∠A＝28°，则∠ACB的度数是（）

A、28° B、30° C、31° D、32°

查看试题解析
7. 已知抛物线 $y = - x^{2} + b x + 4$ 经过 $(- 2, n)$ 和 $(4, n)$ 两点，则n的值为（）

A、﹣2 B、﹣4 C、2 D、4

查看试题解析
8. 如图，矩形ABCD中，AB=8，BC=4.点G，E分别在边AB，CD上，点F，H在对角线AC上.若四边形EFGH是菱形，则AG的长是（）

A、 $2 \sqrt{5}$ B、5 C、 $3 \sqrt{5}$ D、6

查看试题解析
9. 如图，▱OABC的周长为7，∠AOC＝60°，以O为原点，OC所在直线为x轴建立直角坐标系，函数 $y = \frac{k}{x}$ （x＞0）的图像经过▱OABC的顶点A和BC的中点M，则k的值为（）

A、 $4 \sqrt{3}$ B、12 C、 $\sqrt{3}$ D、6

查看试题解析
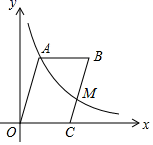10. 如图，在边长为6的等边三角形ABC中，E是对称轴AD上的一个动点，连接CE，将线段CE绕点C逆时针旋转60°得到FC，连接DF.则在点E运动过程中，DF的最小值是（）

A、6 B、3 C、2 D、1.5

查看试题解析

二、填空题

11. 9的平方根是，使分式 $\frac{1}{x + 1}$ 有意义的x的取值范围是．

查看试题解析
12. 港珠澳大桥被英国《卫报》誉为“新世界七大奇迹”之一，它是世界总体跨度最长的跨海大桥，全长55000米.数字55000用科学记数法表示为.

查看试题解析
13. 分解因式：a³﹣2a²+a= ．

查看试题解析
14. 如图，圆锥母线长为6，圆锥的高与母线所夹的角为θ，且sinθ＝ $\frac{1}{3}$ ，该圆锥的侧面积是.

查看试题解析
15. 一次函数y₁＝ax+3与y₂＝kx﹣1的图象如图所示，则不等式kx﹣ax $<$ 4的解集是.

查看试题解析
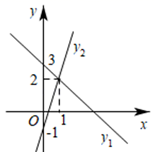16. 如图，在等腰直角三角形ABC中，∠ACB=90°，AB=8，点E是AB的中点，以AE为边作等边△ADE（点D与点C分别在AB异侧），连接CD，则△ACD的面积是.

查看试题解析
17. 在△ABC中，∠A=60°，∠C=75°，AB=8，D、E、F分别在AB、BC、CA上，则△DEF的周长最小值是.

查看试题解析
18. 如图，在平面直角坐标系中，Rt△ABC的顶点B与原点O重合，直角边BC在x轴的正半轴上，∠ACB=90°，点A的坐标为（3， $\sqrt{3}$ ），点D是BC边上一个动点（不与点B，C重合），过点D作DE⊥BC交AB边于点E，将△BDE沿直线DE翻折，点B落在x轴上的点F处，当△AEF为直角三角形时，点F的坐标是.

查看试题解析

三、解答题

19. 计算：

(1)、-1²⁰²⁰+（π﹣3.14）⁰+（ $\frac{1}{2}$ ）^-2；

(2)、2x⁴y⁶-x²•（-2xy³）².

查看试题解析
20. 解方程：

(1)、x²﹣4x＝1

(2)、 $\frac{x - 2}{x + 2} - 1 = \frac{16}{x^{2} - 4}$

查看试题解析
21. 如图，点 $A 、 E 、 F 、 C$ 在一直线上， $D E ∥ B F ， D E = B F ， A E = C F$ .试说明 $A B ∥ C D$ 的理由.

查看试题解析
22. 在一个不透明的盒中有m个黑球和1个白球，这些球除颜色外无其他差别.

(1)、若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子.通过大量重复试验后，发现摸到黑球的频率稳定在0.75左右，则m的值应是；

(2)、在（1）的条件下，用m个黑球和1个白球进行摸球游戏.先从盒中随机摸取一个球，再从剩下的球中再随机摸取一个球，求事件“先摸到黑球，再摸到白球”的概率（请用“画树状图”或“列表”等方法写出分析过程）.

查看试题解析
23. 某校“心灵信箱”的设立，为师、生之间的沟通开设了一个书面交流的渠道．为了解九年级学生对“心灵信箱”开通两年来的使用情况，某课题组对该校九年级全体学生进行了一次问卷调查，并根据调查结果绘制了如下尚不完整的统计图．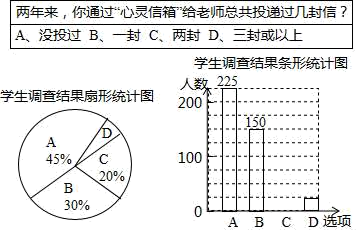

根据图表，解答以下问题：

(1)、该校九年级学生共有人；

(2)、学生调查结果扇形统计图中，扇形D的圆心角度数是；

(3)、请你补充条形统计图；

(4)、根据调查结果可以推断：两年来，该校九年级学生通过“心灵信箱”投递出的信件总数至少有封．

查看试题解析
24. 如图，以△ABC的边AB为直径作⊙O，与BC交于点D，点E是 $\overset{⌢}{B D}$ 的中点，连接AE交BC于点F，∠ACB＝2∠BAE.

(1)、求证：AC是⊙O的切线；

(2)、若sinB＝ $\frac{2}{3}$ ，BD＝5，求BF的长.

查看试题解析
25. 某公司经过市场调查，发现某种运动服的销量与售价是一次函数关系，具体信息如表：

已知该运动服的进价为每件150元.

(1)、售价为x元，月销量为y件.
①求y关于x的函数关系式：

②若销售该运动服的月利润为w元，求w关于x的函数关系式，并求月利润最大时的售价；

(2)、由于运动服进价降低了a元，商家决定回馈顾客，打折销售，这时月销量与调整后的售价仍满足（1）中函数关系式.结果发现，此时月利润最大时的售价比调整前月利润最大时的售价低15元，则a的值是多少？

查看试题解析
26. 如图，将含30°角的直角三角板ABC（∠A＝30°）绕其直角顶点C顺时针旋转α角（0°＜α＜90°），得到Rt△A′B′C，A′C与AB交于点D，过点D作DE∥A′B′交CB′于点E，连接BE.易知，在旋转过程中，△BDE为直角三角形.设BC＝1，AD＝x，△BDE的面积为S.

(1)、当α＝30°时，求x的值.

(2)、求S与x的函数关系式，并写出x的取值范围；

(3)、以点E为圆心，BE为半径作⊙E，当S＝ $\frac{1}{4} S_{Δ A B C}$ 时，判断⊙E与A′C的位置关系，并求相应的tanα值.

查看试题解析
27. 如图1，直线AB与x轴、y轴分别相交于点A、B，将线段AB绕点A顺时针旋转90°，得到AC，连接BC，将△ABC沿射线BA平移，当点C到达x轴时运动停止．设平移距离为m，平移后的图形在x轴下方部分的面积为S，S关于m的函数图象如图2所示（其中0＜m≤a，a＜m≤b时，函数的解析式不同）．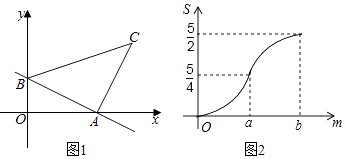

(1)、填空：△ABC的面积为；

(2)、求直线AB的解析式；

(3)、求S关于m的解析式，并写出m的取值范围．

查看试题解析
28. 如图1，在平面直角坐标系中，抛物线y＝ $- \frac{1}{8}$ x²+ $\frac{1}{4}$ x+3与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C，过点C作x轴的平行线交抛物线于点P.连接AC.

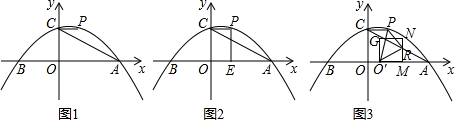(1)、求点P的坐标及直线AC的解析式；

(2)、如图2，过点P作x轴的垂线，垂足为E，将线段OE绕点O逆时针旋转得到OF，旋转角为α（0°＜α＜90°），连接FA、FC.求AF+ $\frac{2}{3}$ CF的最小值；

(3)、如图3，点M为线段OA上一点，以OM为边在第一象限内作正方形OMNG，当正方形OMNG的顶点N恰好落在线段AC上时，将正方形OMNG沿x轴向右平移，记平移中的正方形OMNG为正方形O′MNG，当点M与点A重合时停止平移.设平移的距离为t，正方形O′MNG的边MN与AC交于点R，连接O′P、O′R、PR，是否存在t的值，使△O′PR为直角三角形？若存在，求出t的值；若不存在，请说明理由.

查看试题解析