江苏省常熟市2020年数学中考一模试卷
试卷更新日期:2020-07-30 类型:中考模拟
一、选择题
-
1. 下列四个实数中,无理数是( )A、 B、 C、-2 D、2. 若代数式 在实数范围内有意义,则实数x的取值范围是( )A、 B、 C、 D、3. 据统计,2019年末我市常住人口约为1519000人,将1519000用科学记数法表示为( )A、 B、 C、 D、4. 如图, ,点 在 上,若 , ,则 等于( )
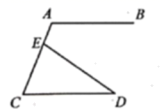 A、70° B、106° C、110° D、146°5. 如图,四边形 内接于 ,点C是 的中点, ,则 的度数为( )
A、70° B、106° C、110° D、146°5. 如图,四边形 内接于 ,点C是 的中点, ,则 的度数为( )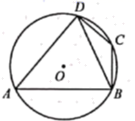 A、20° B、25° C、30° D、35°6. 若一次函数 (k为常数且 )的图像经过点(-2,0),则关于x的方程 的解为( )A、 B、 C、 D、7. 九年级(1)班25名女同学进行排球垫球,每人只测一次,测试结果统计如下表:
A、20° B、25° C、30° D、35°6. 若一次函数 (k为常数且 )的图像经过点(-2,0),则关于x的方程 的解为( )A、 B、 C、 D、7. 九年级(1)班25名女同学进行排球垫球,每人只测一次,测试结果统计如下表:排球垫球(次)
8
12
20
23
24
26
32
36
人数
1
1
2
4
7
6
3
1
这25名女同学排球垫球次数的众数和中位数分别是( )
A、24,26 B、36,23.5 C、24,23.5 D、24,248. 如图,四边形 是矩形, 的平分线交 延长线于点 ,若 , ,则 的长为( )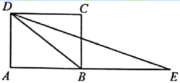 A、4.2 B、4.5 C、5.2 D、5.59. 一艘轮船在A处测得灯塔S在船的南偏东60°方向,轮船继续向正东航行30海里后到达 处,这时测得灯塔S在船的南偏西75°方向,则灯塔S离观测点A、B的距离分别是( )
A、4.2 B、4.5 C、5.2 D、5.59. 一艘轮船在A处测得灯塔S在船的南偏东60°方向,轮船继续向正东航行30海里后到达 处,这时测得灯塔S在船的南偏西75°方向,则灯塔S离观测点A、B的距离分别是( )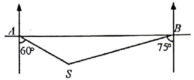 A、 海里、15海里 B、 海里、15海里 C、 海里、 海里 D、 海里、 海里10. 如图, 中, , ,点D在 的延长线上,且 ,连接 并延长,作 于 ,若 ,则△ 的面积为( )
A、 海里、15海里 B、 海里、15海里 C、 海里、 海里 D、 海里、 海里10. 如图, 中, , ,点D在 的延长线上,且 ,连接 并延长,作 于 ,若 ,则△ 的面积为( )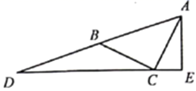 A、8 B、10 C、 D、16
A、8 B、10 C、 D、16二、填空题
-
11. 计算: = .12. 因式分解:a2-9=.13. 关于x的一元二次方程 有两个相等的实数根,则c的值是.14. 若 , ,则a+b的值为.15. 以小正方形的中心为位似中心,以1:3的比例放大得到一个大正方形,从而得到了一个如图所示的飞镖游戏板.若小明同学向该游戏板投掷飞镖一次(假设飞镖落在游戏板上),则镖落在阴影部分的概率是.
 16. 如图,在四边形 中, , , ,以点A为圆心, 为半径的圆与 相切于点E,交 于点F.用扇形 围成一个圆锥的侧面,则这个圆锥底面圆的半径为.
16. 如图,在四边形 中, , , ,以点A为圆心, 为半径的圆与 相切于点E,交 于点F.用扇形 围成一个圆锥的侧面,则这个圆锥底面圆的半径为.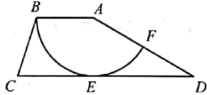 17. 甲、乙两列火车分别从A、B两地出发相向而行,他们距B地的路程 ( )与甲行驶的时间 (h)的函数关系如图所示,那么乙火车的速度是 .
17. 甲、乙两列火车分别从A、B两地出发相向而行,他们距B地的路程 ( )与甲行驶的时间 (h)的函数关系如图所示,那么乙火车的速度是 .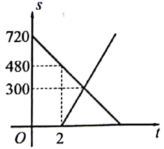 18. 如图, 中, , ,点D在 上( ),将 沿 翻折,得到 , 交 于点F.当 时, 的值为.
18. 如图, 中, , ,点D在 上( ),将 沿 翻折,得到 , 交 于点F.当 时, 的值为.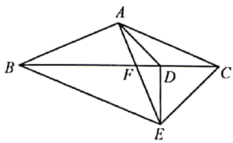
三、解答题
-
19. 计算: .20. 解不等式组:21. 先化简,再求值: ,其中 .22. 如图,在四边形 中, , , , ,垂足为E.
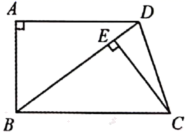 (1)、求证: ;(2)、若 , ,求 的长.23. 初三(1)班针对“垃圾分类”知晓情况对全班学生进行专题调查活动,对“垃圾分类”的知晓情况分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,每名学生可根据自己的情况任选其中一类,班长根据调查结果进行了统计,并绘制成了不完整的条形统计图和扇形统计图.
(1)、求证: ;(2)、若 , ,求 的长.23. 初三(1)班针对“垃圾分类”知晓情况对全班学生进行专题调查活动,对“垃圾分类”的知晓情况分为A、B、C、D四类.其中,A类表示“非常了解”,B类表示“比较了解”,C类表示“基本了解”,D类表示“不太了解”,每名学生可根据自己的情况任选其中一类,班长根据调查结果进行了统计,并绘制成了不完整的条形统计图和扇形统计图.“垃圾分类”知晓情况各类别人数条形统计图 “垃圾分类”知晓情况各类别人数扇形统计图
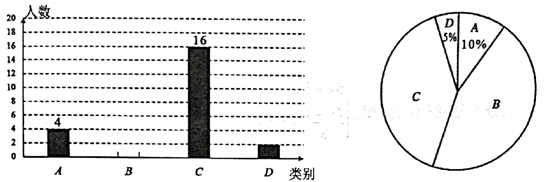
根据以上信息解决下列问题:
(1)、初三(1)班参加这次调查的学生有人,扇形统计图中类别C所对应扇形的圆心角度数为°;(2)、求出类别B的学生数,并补全条形统计图;(3)、类别 的4名学生中有2名男生和2名女生,现从这4名学生中随机选取2名学生参加学校“垃圾分类”知识竞赛,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.24. 某公司销售甲、乙两种品牌的投影仪,这两种投影仪的进价和售价如下表所示:甲
乙
进价(元/套)
3000
2400
售价(元/套)
3300
2800
该公司计划购进两种投影仪若干套,共需66000元,全部销售后可获毛利润9000元.
(1)、该公司计划购进甲、乙两种品牌的投影仪各多少套?(2)、通过市场调研,该公司决定在原计划的基础上,减少甲种投影仪的购进数量,增加乙种投影仪的购进数量,已知乙种投影仪增加的数量是甲种投影仪减少的数量的2倍。若用于购进这两种投影仪的总资金不超过75000元,问甲种投影仪购进数量至多减少多少套?25. 如图,在平面直角坐标系中,矩形 的顶点A,B在x轴的正半轴上,顶点D在直线 位于第一象限的图像上,反比例函数 的图像经过点D,交 于点E, .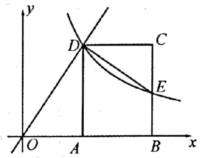 (1)、如果 ,求点E的坐标;(2)、连接 ,当 时,求点D的坐标.26. 如图, 是 的直径, 是弦,点E在圆外, 于 , 交 于点F,连接 , , , .
(1)、如果 ,求点E的坐标;(2)、连接 ,当 时,求点D的坐标.26. 如图, 是 的直径, 是弦,点E在圆外, 于 , 交 于点F,连接 , , , .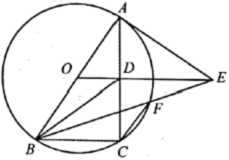 (1)、求证: 是 的切线;(2)、求证: ;(3)、设 的面积为 , 的面积为 ,若 ,求 的值.27. 如图①, 中, ,点D从点A出发沿 方向匀速运动,速度为1 点E是 上位于点D右侧的动点,点M是 上的动点,在运动过程中始终保持 , cm.过M作 交 于N,当点R与点C重合时点D停止运动.设 的面积为 ,点D的运动时间为 ,S与t的函数关系如图②所示:
(1)、求证: 是 的切线;(2)、求证: ;(3)、设 的面积为 , 的面积为 ,若 ,求 的值.27. 如图①, 中, ,点D从点A出发沿 方向匀速运动,速度为1 点E是 上位于点D右侧的动点,点M是 上的动点,在运动过程中始终保持 , cm.过M作 交 于N,当点R与点C重合时点D停止运动.设 的面积为 ,点D的运动时间为 ,S与t的函数关系如图②所示: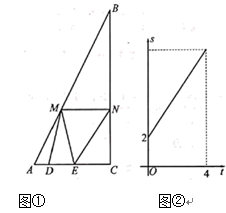 (1)、 = , = ;(2)、设四边形 的面积为y,求y的最大值;(3)、是否存在 的值,使得以M,E,N为顶点的三角形与 相似?如果存在,求 的值;如果不存在,说明理由.28. 如图,二次函数 的图像与x轴交于点A,B(A在B左侧),与y轴正半轴交于点C,点D在抛物线上, 轴,且 .
(1)、 = , = ;(2)、设四边形 的面积为y,求y的最大值;(3)、是否存在 的值,使得以M,E,N为顶点的三角形与 相似?如果存在,求 的值;如果不存在,说明理由.28. 如图,二次函数 的图像与x轴交于点A,B(A在B左侧),与y轴正半轴交于点C,点D在抛物线上, 轴,且 .
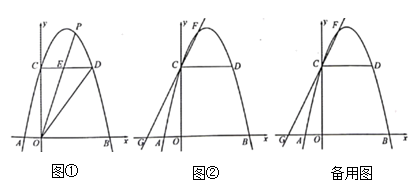 (1)、求点A,B的坐标及a的值;(2)、点P为y轴右侧抛物线上一点.
(1)、求点A,B的坐标及a的值;(2)、点P为y轴右侧抛物线上一点.①如图①,若 平分 , 交 于点E,求点P的坐标;
②如图②,抛物线上一点F的横坐标为2,直线 交x轴于点G,过点P作直线 的垂线,垂足为Q,若 ,求点Q的坐标.