浙江省杭州市下城区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-07-30 类型：期末考试

进入出卷网下载

一、选择题：本大题有10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.

1. 方程2x+y＝1的解可以是（　　）

A、 ${\begin{cases} x = 1 \\ y = 1 \end{cases}$ B、 ${\begin{cases} x = 1 \\ y = - 1 \end{cases}$ C、 ${\begin{cases} x = - 1 \\ y = 1 \end{cases}$ D、 ${\begin{cases} x = - 1 \\ y = - 1 \end{cases}$

查看试题解析
2. 下列各式计算结果正确的是（　　）

A、a²+a³＝2a⁵ B、a²•a³＝a⁶ C、（a²）³＝a⁵ D、（﹣a）²•a³＝a⁵

查看试题解析
3. 如图，直线l₁ ， l₂被直线1₃所截，则（　　）

A、∠1和∠2是同位角 B、∠1和∠2是内错角 C、∠1和∠3是同位角 D、∠1和∠3是内错角

查看试题解析
4. 下列运算正确的是（　　）

A、（x+y）（y﹣x）＝x²﹣y² B、（x+y）（﹣y﹣x）＝x²﹣y² C、（x﹣y）（y﹣x）＝x²﹣y² D、（x+y）（﹣y+x）＝x²﹣y²

查看试题解析
5. 抽样调查放学时段学校附近某路口车流量情况的样本中，下列最合适的是（　　）

A、抽取一月份第一周为样本 B、任意抽一天为样本 C、选取每周日为样本 D、每个季节各选两周作为样本

查看试题解析
6. 如图，在下列给出的条件中，不能判定AB∥DF的是（　　）

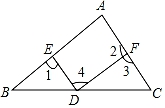A、∠1＝∠A B、∠A＝∠3 C、∠1＝∠4 D、∠A+∠2＝180°

查看试题解析
7. 分式 $\frac{x + 1}{x - 2}$ 的值（　　）

A、不能为﹣1 B、不能为0 C、不能为1 D、不能为2

查看试题解析
8. 下列因式不能整除多项式4x³y+4x²y²+xy³的是（　　）

A、xy B、2x+y C、x²+2xy D、2xy+y²

查看试题解析
9. 如图，AB∥CD，EC分别交AB，CD于点F，C，连结DF，点G是线段CD上的点，连结FG.若∠1＝∠3，∠2＝∠4，则结论①∠C＝∠D；②FG⊥CD； ③EC⊥FD中，正确的是（　　）

A、①② B、②③ C、①③ D、①②③

查看试题解析
10. 若p＝ $\frac{1}{n (n + 2)}$ + $\frac{1}{(n + 2) (n + 4)}$ + $\frac{1}{(n + 4) (n + 6)}$ + $\frac{1}{(n + 6) (n + 8)}$ + $\frac{1}{(n + 8) (n + 10)}$ ，则使p最近 $\frac{1}{10}$ 的正整数n是（　　）

A、4 B、5 C、6 D、7

查看试题解析

二、填空题：本大题有6个小题，每小题4分，共24分.

11. 已知一组数据的频率为0.35，数据总数为500个，则这组数据的频数为．

查看试题解析
12. 如图，已知∠1＝∠2＝∠3＝50°，则∠4＝.

查看试题解析
13. 若a﹣b＝7，ab＝﹣12，则（a+b）²＝.

查看试题解析
14. 已知x＝2y，则分式 $\frac{x - y}{2 x + y}$ 的值为.

查看试题解析
15. 如图，已知a∥b，∠1+∠4＝70°，∠2﹣∠3＝20°则∠1＝.

查看试题解析
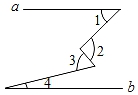16. 已知x²+kx+12＝（x+a）（x+b），x²+kx+15＝（x+c）（x+d），其中a，c，d均为整数.则k＝.

查看试题解析

三、解答题：本大题有7个小题，共66分.解答应写出文字说明、证明过程或演算步骤.

17. 因式分解：

(1)、2x²﹣8.

(2)、4a²﹣12ab+9b².

查看试题解析
18. 解分式方程 $\frac{1 - x}{x - 2} = \frac{1}{2 - x} - 2$ 圆圆的解答如下：
解：去分母，得1﹣x＝﹣1﹣2化简，得x＝4经检验，x＝4是原方程的解.

∴原方程的解为x＝4.

圆圆的解答正确吗？如果不正确，写出正确的解答.

查看试题解析
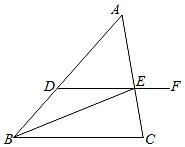
19. 水果市场出售枇杷，枇杷分成三个等级：优质果，二级果，三级果.根据某一天枇杷的销售量制成了如图的统计图.

(1)、补全条形统计图.

(2)、求出图1二级果扇形的圆心角的度数.

(3)、若优质果，二级果，三级果，单价分别为15元/斤，10元/斤，5元/斤，该水果市场这一天销售枇杷的总金额是多少元？

查看试题解析
20. 如图，AD是∠BAC的角平分线，点E是射线AC上一点，延长ED至点F，∠CAD+∠ADF＝180°

求证：

(1)、AB∥EF.

(2)、2∠ADE＝∠CEF.

查看试题解析
21. 某场篮球赛，门票共两种，价格为：成人票30元/张，儿童票10元/张；门票总收入：4700元.

(1)、若售出门票总数160张，求售出的成人票张数.

(2)、设售出门票总数a张，其中儿童票b张.
①求a，b满足什么数量关系.

②若售出的门票中成人票比儿童票的7倍还多10张，求b的值.

查看试题解析
22. 关于x，y的二元一次方程ax+by＝c（a，b，c是常数），b＝a+1，c＝b+1.

(1)、当 ${\begin{cases} x = 3 \\ y = 1 \end{cases}$ 时，求c的值.

(2)、当a＝ $\frac{1}{2}$ 时，求满足|x|＜5，|y|＜5的方程的整数解.

(3)、若a是正整数，求证：仅当a＝1时，该方程有正整数解.

查看试题解析
23. 如图，在△ABC中，点E在AC边上，连结BE，过点E作DF∥BC，交AB于点D.若BE平分∠ABC，EC平分∠BEF.设∠ADE＝α，∠AED＝β.

(1)、当β＝80°时，求∠DEB的度数.

(2)、试用含α的代数式表示β.

(3)、若β＝kα（k为常数），求α的度数（用含k的代数式表示）.

查看试题解析