湖北省随州市广水市2020年数学中考适应性试卷（5月）

试卷更新日期：2020-07-30 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣ $\frac{1}{5}$ 的相反数是（）

A、﹣5 B、5 C、﹣ $\frac{1}{5}$ D、 $\frac{1}{5}$

查看试题解析
2. 截止2020年3月全国共计确诊8万多例，国家累计投入疫情防控资金累计达1169亿元.把1169亿元用科学记数法表示为（）

A、1.169×10¹⁰元 B、1.169×10¹¹元 C、1.169×10¹²元 D、1.169×10¹³元

查看试题解析
3. 如图，将三角尺的直角顶点放在直尺的一边上，∠1=30°，∠2=50°，则∠3的度数等于（）

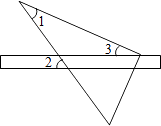A、50° B、30° C、20° D、15°

查看试题解析
4. 下列运算正确的是（）

A、a³•a²=a⁵ B、（a²）³=a⁵ C、a³+a³=a⁶ D、（a+b）²=a²+b²

查看试题解析
5. 从正五边形的五个顶点中，任取四个顶点连成四边形，则这个四边形是等腰梯形的概率是（）

A、1 B、 $\frac{2}{5}$ C、 $\frac{1}{5}$ D、0

查看试题解析
6. 如图，是某几何体的三视图及相关数据，则该几何体的表面积是（）

A、39π B、29π C、24π D、19π

查看试题解析
7. 如图，△ABC内接于⊙O，AB是⊙O的直径，直线AE是⊙O的切线，CD平分∠ACB，若∠CAE=21°，则∠BFC的度数为（）

A、66° B、111° C、114° D、119°

查看试题解析
8. 春节期间，王老师一家自驾游去了离家170千米的某地，下面是他们家的距离y（千米）与汽车行驶时间x（小时）之间的函数图象，当他们离目的地还有20千米时，汽车一共行驶的时间是（）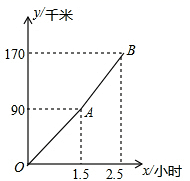

A、2小时 B、2.2小时 C、2.25小时 D、2.4小时

查看试题解析
9. 已知 $C_{3}^{2}$ = $\frac{3 \times 2}{1 \times 2}$ =3， ${C_{5}}^{3}$ = $\frac{5 \times 4 \times 3}{1 \times 2 \times 3}$ =10， $C_{6}^{4}$ = $\frac{6 \times 5 \times 4 \times 3}{1 \times 2 \times 3 \times 4}$ =15，……观察以上计算过程，寻找规律.计算 C₈5=（）

A、72 B、56 C、42 D、40

查看试题解析
10. 二次函数 $y$ ＝ $a x^{2} + b x + c$ （ $a$ ≠0）图象如图所示，下列结论：① $a b c$ ＞0；② $2 a + b$ ＝0；③当 $m$ ≠1时，a+b＞ $a m^{2} + b m$ ；④ $a - b + c$ ＞0；⑤若 $a x_{1}^{2} + b x_{1}$ ＝ $a x_{2}^{2} + b x_{2}$ ，且 $x_{1}$ ≠ $x_{2}$ ，则 $x_{1} + x_{2}$ ＝2.其中正确的有（）

A、①②③ B、②④ C、②⑤ D、②③⑤

查看试题解析

二、填空题

11. 分解因式：a²﹣a﹣6=.

查看试题解析
12. 已知一组数据0，2，x，4，5的众数是4，那么这组数据的中位数是.

查看试题解析
13. 《九章算术》是我国古代数学名著，卷七“盈不足”中有题译文如下：今有人合伙买羊，每人出5钱，会差45钱；每人出7钱，会差3钱.问合伙人数、羊价各是多少？设合伙人数为x人，所列方程为.

查看试题解析
14. 如图，直线 $y = - \frac{4}{3} x + 4$ 与x轴、y轴分别交于A、B两点，把△AOB绕点A顺时针旋转90°后得到△AO′B′，则点B′的坐标是。

查看试题解析
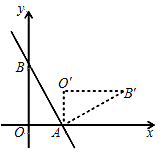15. 如图，Rt△AOB的一条直角边OB在x轴上，双曲线y= $\frac{k}{x}$ （x>0）经过斜边OA的中点C，与另一直角边交于点D.若S_△_OCD=9，则S_△_OBD的值为.

查看试题解析
16. 如图，正方形ABCD中，O为BD中点，以BC为边向正方形内作等边△BCE，连接AE并延长交CD于F，连接BD分别交CE、AF于G、H，下列结论：① $∠ C E H = 45 °$ ；② $B G = \sqrt{2} D G$ ；③ $G F // E D$ ；④ $2 O H + D H = B D$ ；⑤ $S_{△ B E C}$ ： $S_{△ B G C} = \frac{\sqrt{3} + 1}{2}$ ，其中正确的是.

查看试题解析

三、解答题

17. 已知 $\frac{n}{m} = \frac{5}{3}$ ，求式子 $(\frac{m}{m + n} - \frac{m}{m - n}) \div \frac{n^{2}}{m^{2} - n^{2}}$ 的值.

查看试题解析
18. 已知关于x的一元二次方程x²－2 $\sqrt{2}$ x+m=0有两个不相等的实数根.

(1)、求实数m的最大整数值；

(2)、在（1）的条件下，方程的实数根是 $x_{1}$ 、 $x_{2}$ ，求代数式 $x_{1}^{2} + x_{2}^{2} - x_{1} x_{2}$ 的值.

查看试题解析
19. 某中学积极组织学生开展课外阅读活动，为了解本校学生每周课外阅读的时间量t（单位：小时），采用随机抽样的方法抽取部分学生进行了问卷调查，调查结果按0≤t＜2，2≤t＜3，3≤t＜4，t≥4分为四个等级，并分别用A、B、C、D表示，根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图，由图中给出的信息解答下列问题：

(1)、求出x的值，并将不完整的条形统计图补充完整；

(2)、若该校共有学生2500人，试估计每周课外阅读时间量满足2≤t＜4的人数；

(3)、若本次调查活动中，九年级（1）班的两个学习小组分别有3人和2人每周阅读时间量都在4小时以上，现从这5人中任选2人参加学校组织的知识抢答赛，求选出的2人来自不同小组的概率.

查看试题解析
20. 海中两个灯塔A、B，其中B位于A的正东方向上，渔船跟踪鱼群由西向东航行，在点C处测得灯塔A在西北方向上，灯塔B在北偏东30°方向上，渔船不改变航向继续向东航行30海里到达点D，这时测得灯塔A在北偏西60°方向上，求灯塔A、B间的距离.（计算结果用根号表示，不取近似值）

查看试题解析
21. 如图，已知，⊙O为△ABC的外接圆，BC为直径，点E在AB上，过点E作EF⊥BC，点G在FE的延长线上，且GA=GE.

(1)、求证：AG与⊙O相切.

(2)、若AC=6，AB=8，BE=3，求线段OE的长.

查看试题解析
22. 襄阳市精准扶贫工作已进入攻坚阶段．贫困户张大爷在某单位的帮扶下，把一片坡地改造后种植了优质水果蓝莓，今年正式上市销售．在销售的30天中，第一天卖出20千克，为了扩大销量，采取了降价措施，以后每天比前一天多卖出4千克．第x天的售价为y元/千克，y关于x的函数解析式为 ${\begin{matrix} m x - 76 m (1 \leq x < 20 ， x 为整数) \\ n (20 \leq x \leq 30 ， x 为整数) \end{matrix}$ 且第12天的售价为32元/千克，第26天的售价为25元/千克．已知种植销售蓝莓的成木是18元/千克，每天的利润是W元（利润=销售收入﹣成本）．

(1)、m= ， n=；

(2)、求销售蓝莓第几天时，当天的利润最大？最大利润是多少？

(3)、在销售蓝莓的30天中，当天利润不低于870元的共有多少天？

查看试题解析
23. 如图1，在四边形ABCD中，∠DAB被对角线AC平分，且AC²=AB·AD，我们称该四边形为“可分四边形”，∠DAB称为“可分角”.

(1)、如图2，四边形ABCD为“可分四边形”，∠DAB为“可分角”，如果∠DCB=∠DAB，则∠DAB=.

(2)、如图3，在四边形ABCD中，∠DAB=60°，AC平分∠DAB，且∠BCD=150°，求证：四边形ABCD为“可分四边形”；

查看试题解析
24. 如图，抛物线 $y = a x^{2} + b x + c$ 经过点 $A (- 2 ， 5)$ ，与x轴相交于 $B (- 1 ， 0)$ ， $C (3 ， 0)$ 两点，

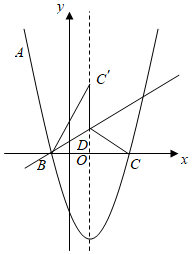(1)、抛物线的函数表达式；

(2)、点D在抛物线的对称轴上，且位于x轴的上方，将 $Δ B C D$ 沿沿直线 $B D$ 翻折得到 $Δ B C^{'} D$ ，若点 $D^{'}$ 恰好落在抛物线的对称轴上，求点 $C^{'}$ 和点D的坐标；

(3)、设P是抛物线上位于对称轴右侧的一点，点Q在抛物线的对称轴上，当 $Δ C P Q$ 为等边三角形时，求直线 $B P$ 的函数表达式.

查看试题解析