湖北省黄冈市2020年数学中考二模试卷
试卷更新日期:2020-07-30 类型:中考模拟
一、选择题
-
1. 绝对值等于9的数是( )A、9 B、-9 C、9或-9 D、2. 根据制定中的通州区总体规划,将通过控制人口总量上限的方式,努力让副中心远离“城市病”.预计到2035年,副中心的常住人口规模将控制在130万人以内,初步建成国际一流的和谐宜居现代化城区.130万用科学记数法表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 下列几何体是由4个相同的小正方体搭成的,其中左视图与主视图相同的是A、
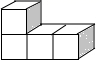 B、
B、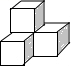 C、
C、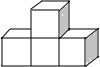 D、
D、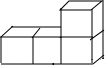 5. 如图,若将线段AB平移至A1B1 , 则a+b的值为( )
5. 如图,若将线段AB平移至A1B1 , 则a+b的值为( )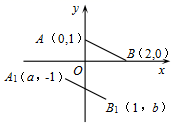 A、﹣3 B、3 C、﹣2 D、06. 已知 , 是一元二次方程 的两个实数根且 ,则 的值为( ).A、0或1 B、0 C、1 D、-17. 如图,在 中, , , 是 的平分线,经过A,D两点的圆的圆心O恰好落在 上, 分别与 、 相交于点E、F.若圆半径为2.则阴影部分面积( ).
A、﹣3 B、3 C、﹣2 D、06. 已知 , 是一元二次方程 的两个实数根且 ,则 的值为( ).A、0或1 B、0 C、1 D、-17. 如图,在 中, , , 是 的平分线,经过A,D两点的圆的圆心O恰好落在 上, 分别与 、 相交于点E、F.若圆半径为2.则阴影部分面积( ).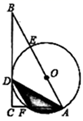 A、 B、 C、 D、8. 如图①,在 中, ,动点D从点A出发,沿 以 的速度匀速运动到点B,过点D作 于点E,图②是点D运动时, 的面积 随时间 变化的关系图象,则 的长为( )
A、 B、 C、 D、8. 如图①,在 中, ,动点D从点A出发,沿 以 的速度匀速运动到点B,过点D作 于点E,图②是点D运动时, 的面积 随时间 变化的关系图象,则 的长为( )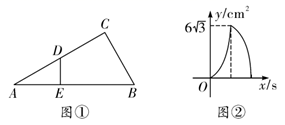 A、4 B、6 C、8 D、10
A、4 B、6 C、8 D、10二、填空题
-
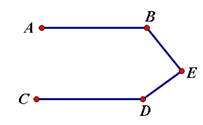
9. 单项式 的次数是.10. 如图,AB∥CD, , ,则 等于 .
 11. 分解因式 .12. 样本数据﹣2,0,3,4,﹣1的中位数是.13. 如图,矩形 的边长 , ,E为 的中点, 分别与 , 相交于点M,N,则 的长为.
11. 分解因式 .12. 样本数据﹣2,0,3,4,﹣1的中位数是.13. 如图,矩形 的边长 , ,E为 的中点, 分别与 , 相交于点M,N,则 的长为.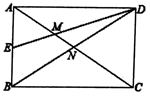 14. 如图所示,矩形纸片 中, ,把它分割成正方形纸片 和矩形纸片 后,分别裁出扇形 和半径最大的圆,恰好能作一个圆锥的侧面和底面,则 的长为.
14. 如图所示,矩形纸片 中, ,把它分割成正方形纸片 和矩形纸片 后,分别裁出扇形 和半径最大的圆,恰好能作一个圆锥的侧面和底面,则 的长为.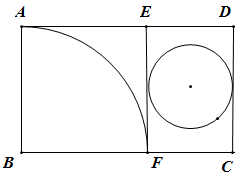 15. 如图,点A在双曲线 上,点B在双曲线 上, 轴,过点A作 轴于D,连接 ,与 相交于点C,若 ,则k的值为.
15. 如图,点A在双曲线 上,点B在双曲线 上, 轴,过点A作 轴于D,连接 ,与 相交于点C,若 ,则k的值为.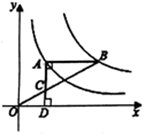 16. 如图,在△ABC中,AC=BC=4 ,∠C=90°,点D在BC上,且CD=3DB,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值是.
16. 如图,在△ABC中,AC=BC=4 ,∠C=90°,点D在BC上,且CD=3DB,将△ABC折叠,使点A与点D重合,EF为折痕,则tan∠BED的值是.
三、解答题
-
17. 先化简,再求值: ,其中 .18. 解不等式组:19. 如图,在▱ABCD中,点E是BC上的一点,连接DE , 在DE上取一点F使得∠AFE=∠ADC . 若DE=AD , 求证:DF=CE .
 20. 甲、乙两车分别从 两地同时出发,沿同一公路相向而行,开往 两地.已知甲车每小时比乙车每小时多走 ,且甲车行驶 所用的时间与乙车行驶 所用的时间相同.(1)、求甲、乙两车的速度各是多少 ?(2)、实际上,甲车出发后,在途中因车辆故障耽搁了20分钟,但仍比乙车提前1小时到达目的地.求 两地间的路程是多少 ?21. 央视“经典咏流传”开播以来受到社会广泛关注,我市也在各个学校开展了传承经典的相关主题活动“戏曲进校园”.某校对此项活动的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图,请你根据统计图所提供的信息解答下列问题:
20. 甲、乙两车分别从 两地同时出发,沿同一公路相向而行,开往 两地.已知甲车每小时比乙车每小时多走 ,且甲车行驶 所用的时间与乙车行驶 所用的时间相同.(1)、求甲、乙两车的速度各是多少 ?(2)、实际上,甲车出发后,在途中因车辆故障耽搁了20分钟,但仍比乙车提前1小时到达目的地.求 两地间的路程是多少 ?21. 央视“经典咏流传”开播以来受到社会广泛关注,我市也在各个学校开展了传承经典的相关主题活动“戏曲进校园”.某校对此项活动的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图,请你根据统计图所提供的信息解答下列问题:
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”.
(1)、被调查的总人数是 ▲ 人,扇形统计图中B部分所对应的扇形圆心角的度数为 ▲ , 并补全条形统计图;(2)、若该校共有学生1800人,请根据上述调查结果估计该校学生中A类有多少人;(3)、在A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树状图或列表法求出被抽到的两个学生性别相同的概率.22. 如图1,我国古建筑的大门上常常悬挂着巨大的匾额,图2中的线段 就是悬挂在墙壁AM上的某块匾额的截面示意图.已知 米, .从水平地面点D处看点C,仰角 ,从点 处看点 ,仰角 .且 米,求匾额悬挂的高度 的长.(参考数据: , , )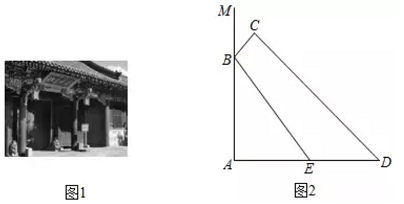 23. 如图,△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D。
23. 如图,△ABC是⊙O的内接三角形,∠ACB=45°,∠AOC=150°,过点C作⊙O的切线交AB的延长线于点D。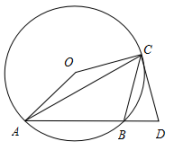 (1)、求证:CD=CB。(2)、如果⊙O的半径为2,求AC的长。24. 某商场秋季计划购进一批进价为每件40元的 恤进行销售.(1)、根据销售经验,应季销售时,若每件 恤的售价为60元,可售出400件;若每件 恤的售价每提高1元,销售量相应减少10件.
(1)、求证:CD=CB。(2)、如果⊙O的半径为2,求AC的长。24. 某商场秋季计划购进一批进价为每件40元的 恤进行销售.(1)、根据销售经验,应季销售时,若每件 恤的售价为60元,可售出400件;若每件 恤的售价每提高1元,销售量相应减少10件.①假设每件 恤的售价提高 元,那么销售每件 恤所获得的利润是 ▲ 元,销售量是 ▲ 件(用含x的代数式表示);
②设应季销售利润为y元,请写y与x的函数关系式;并求出应季销售利润为8000元时每件T恤的售价.
(2)、根据销售经验,过季处理时,若每件 恤的售价定为30元亏本销售,可售出50件;若每件T恤的售价每降低1元,销售量相应增加5条.①若剩余100件T恤需要处理,经过降价处理后还是无法销售的只能积压在仓库,损失本金;若使亏损金额最小,每件T恤的售价应是多少元?
②若过季需要处理的T恤共m件,且 ,季亏损金额最小是 ▲ 元(用含m的代数式表示).
25. 如图,一条抛物线与 轴交于 , 两点,与 轴交于点 , 为抛物线的顶点,点 在 轴上.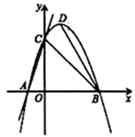
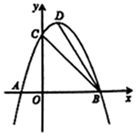 (1)、求抛物线解析式;(2)、若 ,求点 的坐标;(3)、过点 作直线 交抛物线于Q,是否存在以点A,P,Q,C为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由;(4)、坐标平面内一点M到点 的距离为1个单位,求 的最小值.
(1)、求抛物线解析式;(2)、若 ,求点 的坐标;(3)、过点 作直线 交抛物线于Q,是否存在以点A,P,Q,C为顶点的四边形是平行四边形?若存在,请求出点Q的坐标;若不存在,请说明理由;(4)、坐标平面内一点M到点 的距离为1个单位,求 的最小值.