湖北省恩施州2020年数学中考适应性试卷
试卷更新日期：2020-07-30 类型：中考模拟
一、选择题
-
1. -2020的相反数等于（ ）A、-2020 B、 C、 D、20202. 随着我国金融科技的不断发展，网络消费、网上购物已成为人们生活不可或缺的一部分，今年“双十一”天猫成交额高达2135亿元.将数据“2135亿”用科学记数法表示为（ ）A、2.135×1011 B、2.135×107 C、2.135×1012 D、2.135×1033. 下列文化体育活动的图案中，是轴对称图形的是（ ）A、
B、
C、
D、
4. 下列计算正确的是（ ）A、（﹣2a）3＝﹣2a3 B、（﹣a﹣b）（a﹣b）＝b2﹣a2 C、（a+b）2＝a2+b2 D、（﹣a）2•（﹣a）3＝a65. 某单位招考技术人员，考试分笔试和面试两部分，笔试成绩与面试成绩按 记入总成绩，若小李笔试成绩为80分，面试成绩为90分，则他的总成绩为（ ）A、84分 B、85分 C、86分 D、87分6. 如图，在△ABC中，点D，E，F分别是AB，AC，BC的中点，已知∠ADE=65°，则∠CFE的度数为（ ）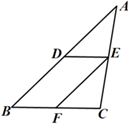
A、60° B、65° C、70° D、75°7. 在关于x的函数 中，自变量x的取值范围是（ ）A、x≥﹣2 B、x≥﹣2且x≠0 C、x≥﹣2且x≠1 D、x≥18. 如图是几何体的俯视图，所表示数字为该位置小正方体的个数，则该几何体的主视图是（ ）
A、
B、
C、
D、
9. 为了宣传垃圾分类，童威写了一篇倡议书，决定用微博转发的方式传播.他设计了如下的传播规则：将倡议书发表在自己的微博上，再邀请n个好友转发，每个好友转发之后，又邀请n个互不相同的好友转发，依次类推.已知经过两轮转发后，共有111个人参与了宣传活动，则n的值为（ ）A、9 B、10 C、11 D、1210. 若关于x的不等式 有且只有三个整数解，则实数a的取值范围是（ ）A、15＜a≤18 B、5＜a≤6 C、15≤a＜18 D、15≤a≤1811. 如图，矩形ABCD，沿对角线BD翻折△BCD，点E是点C的落点，BE交AD于点F，若CD＝4，EF＝3，则BD的长为（ ）
A、5 B、5 C、4 D、1012. 如图，二次函数y＝ax2+bx+c（a≠0）的图象与x轴交于A，B两点，点B位于（4，0）、（5，0）之间，与y轴交于点C，对称轴为直线x＝2，直线y＝﹣x+c与抛物线y＝ax2+bx+c交于C，D两点，D点在x轴上方且横坐标小于5，则下列结论：①4a+b+c＞0；②a﹣b+c＜0；③m（am+b）＜4a+2b（其中m为任意实数）；④a＜﹣1，其中正确的是（ ）
A、①②③④ B、①②③ C、①②④ D、①③④二、填空题
-
13. 计算：0.09的平方根是.14. 因式分解： =.15. 如图，在△ABC中，AB=4，若将△ABC绕点B顺时针旋转60°，点A的对应点为点A′，点C的对应点为点C′，点D为A′B的中点，连接AD.则点A的运动路径 与线段AD、A′D围成的阴影部分面积是.
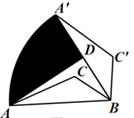16. 将正整数按照图示方式排列，请写出“2020”在第行左起第个数.
三、解答题
-
17. 先化简，再求值：（ ） ，其中x＝ +1.18. 如图，在四边形ABCD中，AD∥BC，点O是对角线AC的中点，过点O作AC的垂线，分别交AD、BC于点E、F，连接AF、CE.试判断四边形AECF的形状，并证明.
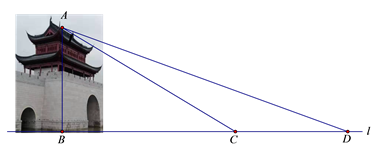
19. 为了解某中学学生课余活动情况，对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计，现从该校随机抽取 名学生作为样本，采用问卷调查的方式收集数据(参与问卷调查的每名学生只能选择其中一项)，并据调查得到的数据绘制成了如图所示的两幅不完整的统计图，由图中提供的信息，解答下列问题：
(1)、 ▲ ， 直接补全条形统计图；(2)、若该校共有学生3200名，试估计该校喜爱看课外书的学生人数；(3)、若被调查喜爱体育活动的4名学生中有3名男生和1名女生，现从这4名学生中任意抽取2名，请用列表或画树状图的方法求恰好抽到2名男生的概率.20. 水城门位于淀浦河和漕港河三叉口，是环城水系公园淀浦河梦蝶岛区域重要的标志性景观．在课外实践活动中，某校九年级数学兴趣小组决定测量该水城门的高．他们的操作方法如下：如图，先在D处测得点A的仰角为20°，再往水城门的方向前进13米至C处，测得点A的仰角为31°（点D、C、B在一直线上），求该水城门AB的高．（精确到0.1米）（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）
21. 如图， 的直角顶点 为坐标原点， ，点A在反比例函数 的图象上，点 在反比例函数 的图象上， 交y轴于点C，C为 中点.
(1)、求点A的坐标；(2)、求 的面积；(3)、求k的值.22. 为建设最美恩施，一旅游投资公司拟定在某景区用茶花和月季打造一片人工花海，经市场调查，购买3株茶花与4株月季的费用相同，购买5株茶花与4株月季共需160元.(1)、求茶花和月季的销售单价；(2)、该景区至少需要茶花月季共2200株，要求茶花比月季多400株，但订购两种花的总费用不超过50000元，该旅游投资公司怎样购买所需总费用最低，最低费用是多少.23. 如图，已知AB为⊙O的直径，AC为⊙O的切线，连接CO，过B作BD//OC交⊙O于D，连接AD交OC于G，延长AB、CD交于点E.
(1)、求证：CD是⊙O的切线；(2)、若BE＝4，DE＝8，①求CD的长；
②连接BC交AD于F，求 的值.
24. 如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴是 ，且经过A（﹣4，0），C（0，2）两点，直线l：y=kx+t（k≠0）经过A，C.
(1)、求抛物线和直线l的解析式；(2)、点P是直线AC上方的抛物线上一个动点，过点P作PD⊥x轴于点D，交AC于点E，过点P作PF⊥AC，垂足为F，当△PEF≌△AED时，求出点P的坐标；(3)、在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，直接写出所有满足条件的Q点的坐标；若不存在，请说明理由.