河南省禹州市2019-2020学年七年级上学期“三科联赛”数学试卷

试卷更新日期：2020-07-30 类型：竞赛测试

进入出卷网下载

一、选择题

1. 在有理数中，有（）

A、绝对值最大的数 B、相反数最大的数 C、倒数最小的数 D、绝对值最小的数

查看试题解析
2. 一个整数 $80160 \dots 0$ 用科学记数法表示为 $8.016 \times 10^{12}$ ，则原数中“0”的个数为（）

A、8 B、9 C、10 D、11

查看试题解析
3. 下列说法：①若a、b互为相反数，则 $a b < 0$ ；②若 $\frac{a}{5 b} = - \frac{1}{5}$ ，则a、b互为相反数；③一个数的平方是它本身，则这个数为0或1；④若 $- 1 < a < 0$ ，则 $a^{2} > - \frac{1}{a}$ ，其中正确的是（）

A、②③ B、①② C、①③④ D、②③④

查看试题解析
4. 如果单项式 $7 x^{m} y^{n + 2}$ 与单项式 $4 x^{2 - m} y^{3 n - 1}$ 是同类项，则 $m - 2 n$ 的值是（）

A、1 B、-1 C、2 D、-2

查看试题解析
5. 有一口水井，水面比井口低 $1 m$ ，一只蜗牛从水面沿井壁往井口爬，它每天白天向上爬行 $32 c m$ ，但每天晚上又下滑 $20 c m$ ，蜗牛爬出井口需要的天数是（）

A、6天 B、7天 C、8天 D、9天

查看试题解析
6. 在数轴上点 $A$ 、 $B$ 所表示的数分别为-2和5，点C在数轴上，且点C到点A、B的距离之和为13，则点C所表示的数为（）

A、-5 B、8 C、-5或8 D、3或-8

查看试题解析
7. 定义：若 $a + b = n$ ，则称a与b是关于数n的“平衡数”. 比如3与-4是关于-1的“平衡数”，5与12是关于17的“平衡数”. 现有 $a = 3 x^{2} - 10 k x + 12$ 与 $b = - 3 x^{2} + 5 x - 2 k$ （k为常数）始终是关于数n的“平衡数”，则 $n =$ （）

A、11 B、12 C、13 D、14

查看试题解析
8. 若 $(m^{2} - 9) x^{2} + (m + 3) x + 12 = 0$ 是关于 $x$ 的一元一次方程，则 ${(2 x + m)}^{2019} =$ （）

A、1 B、-1 C、 $7^{2019}$ D、 $- 7^{2019}$

查看试题解析
9. 张三经营一家小商店，一天一位顾客用一张50元的人民币买烟，一盒烟18元，张三找了顾客32元钱，过了一会，张三发现刚才那张50元钱是假币. 若张三卖一盒烟能赚3元钱，在这笔买卖中，张三赔了（）

A、64元 B、52元 C、48元 D、47元

查看试题解析
10. 数列 $1 ， 1 ， 2 ， 3 ， 5 ， 8 ， 13 ， 21$ ……的排列规律是：从第3个数开始，每一个数都是它前面两个数的和，这个数列叫做斐波那契数列，在斐波那契数列的前2018个数中，共出现的偶数的个数为（）

A、670 B、671 C、672 D、673

查看试题解析

二、填空题

11. 已知 $a$ 、 $b$ 互为倒数， $c$ 为最小的正整数， $d$ 是最大的负整数， $| x + 5 | = 0$ ，则式子 $3 a b - x^{2} + \frac{c + d}{x}$ 的值为.

查看试题解析
12. 当 $x = - 1$ 时，代数式 $2 a x^{3} - 7 b x - 5$ 的值为3，则 $21 b - 6 a + 10 =$ .

查看试题解析
13. 把四张大小相同的长方形卡片（如图①）按图②、图③两种放法放在一个底面为长方形（长为m，宽为n）的盒底上，底面未被卡片覆盖的部分用阴影表示，若记图②中阴影部分的周长为 $C_{2}$ ，图③中阴影部分的周长为 $C_{3}$ ，则 $C_{2} - C_{3} =$ .

查看试题解析
14. 长度相等而粗细不同的两只蜡烛，其中一支可燃5小时，另一支可燃7小时. 将这两支蜡烛同时点燃，当余下的长度中，一支是另一支的3倍时，蜡烛点燃了小时.

查看试题解析
15. 规定：用 ${m}$ 表示大于 $m$ 的最小整数，例如 ${\frac{5}{2}} = 3$ ， ${4} = 5$ ， ${- 1.5} = - 1$ 等；用 $[m]$ 表示不大于 $m$ 的最大整数，例如 $[\frac{7}{2}] = 3$ ， $[2] = 2$ ， $[- 3.2] = - 4$ ，如果整数 $x$ 满足关系式： $2 {x} + 3 [x] = 32$ ，则 $x =$ .

查看试题解析

三、解答题

16. 计算： $[- \frac{9}{7} \times (- 3 \frac{1}{2}) - 1] \div 25 \div \frac{1}{{(1.25)}^{2}} - | 2 + {(- \frac{1}{2})}^{3} \times 5^{2} |$ .

查看试题解析
17. 若 ${(a + 3)}^{2} + | b - 2 | = 0$ ，求 $3 a b^{2} - {2 a^{2} b - [5 a b^{2} - (6 a b^{2} - 2 a^{2} b)]}$ 的值.

查看试题解析
18. 已知 $c < 0 < a$ ， $a b < 0$ ， $| c | > | a | > | b |$ ，化简： $| b | - | a + b | - | c - a | + | b - c |$ .

查看试题解析
19. 解方程，

(1)、 $\frac{0.1 x + 0.03}{0.2} - \frac{0.2 x - 0.03}{0.3} + \frac{3}{4} = 0$

(2)、 $\frac{2014 - x}{2013} + \frac{2016 - x}{2015} = \frac{2018 - x}{2017} + \frac{2020 - x}{2019}$

查看试题解析
20. 如果关于 $x$ 的方程 $\frac{3 x + 5}{2} - 7 = \frac{2 x - a}{3} - 1$ 的解比方程 $4 x - (3 a + 1) = 6 x + 2 a + 1$ 的解大1，求式子 $a^{2} - 4 a + 1$ 的值.

查看试题解析
21. 已知 $f (x) = a_{1} x^{n} + a_{2} x^{n - 1} + \dots + a_{n - 1} x^{2} + a_{n} x + c$ （其中 $a_{1} ， a_{2} ， \dots ， a_{n}$ 是各项的系数， $c$ 是常数项），我们规定 $f (x)$ 的伴随多项式是 $g (x)$ ，且 $g (x) = n a_{1} x^{n - 1} + (n - 1) a_{2} x^{n - 2} + \dots + 2 a_{n - 1} x + a_{n}$ . 如 $f (x) = 4 x^{3} - 3 x^{2} + 5 x - 8$ ，则它的伴随多项式 $g (x) = 3 \times 4 x^{2} - 2 \times 3 x + 1 \times 5 = 12 x^{2} - 6 x + 5$ .
请根据上面的材料，完成下列问题：

(1)、已知 $f (x) = x^{5}$ ，则它的伴随多项式 $g (x) =$ .

(2)、已知 $f (x) = 5 x^{2} - 3 (9 x - 1)$ ，则它的伴随多项式 $g (x) =$ ；若 $g (x) = 13$ ，x=

(3)、已知二次多项式 $f (x) = (a + 3) x^{2} + 16 x + 21$ ，并且它的伴随多项式是 $g (x)$ ，若关于 $x$ 的方程 $g (x) = - 2 x$ 有正整数解，求 $a$ 的整数值.

查看试题解析
22. 实验室里，水平桌面上有甲、乙、丙三个相同高度的圆柱形容器（容器足够高），底面积之比为 $1 ： 3 ： 1$ ，用两个相同的管子在 $6 c m$ 高度处连通（即管子底部离容器底 $6 c m$ ），现三个容器中，只有甲中有水，水位高 $1 c m$ ，如图所示. 若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升 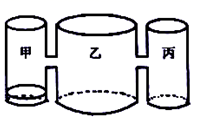$\frac{4}{5} c m$ .

(1)、开始注水1分钟，丙的水位上升 $c m$ ；

(2)、求出开始注入多少分钟的水量后，甲与乙的高度之差是 $0.5 c m$ ？

查看试题解析