河南省平顶山市汝州市2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期:2020-07-30 类型:期末考试
一、选择题
-
1. 下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )A、1 B、2 C、8 D、114. 如图所示,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30′,则下列结论中不正确的是( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 已知三角形两边的长分别是3和7,则此三角形第三边的长可能是( )A、1 B、2 C、8 D、114. 如图所示,直线AB,CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°30′,则下列结论中不正确的是( ) A、∠2=45° B、∠1=∠3 C、∠AOD与∠1互为邻补角 D、∠1的余角等于75°30′5. 下列四个图形中,线段BE是△ABC的高的是( )A、
A、∠2=45° B、∠1=∠3 C、∠AOD与∠1互为邻补角 D、∠1的余角等于75°30′5. 下列四个图形中,线段BE是△ABC的高的是( )A、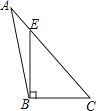 B、
B、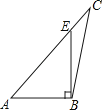 C、
C、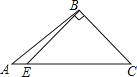 D、
D、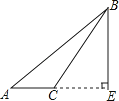 6. 如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
6. 如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( ) A、120° B、125° C、127° D、104°7. 下列说法正确的是( )A、任意掷一枚质地均匀的硬币10次,一定有5次正面向上 B、“等腰三角形的一个角是80度,则它的顶角是80度”是必然事件 C、“篮球队员在罚球线上投篮一次,投中”为随机事件 D、“ 是有理数, ”是不可能事件8. 已知,如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的有( )
A、120° B、125° C、127° D、104°7. 下列说法正确的是( )A、任意掷一枚质地均匀的硬币10次,一定有5次正面向上 B、“等腰三角形的一个角是80度,则它的顶角是80度”是必然事件 C、“篮球队员在罚球线上投篮一次,投中”为随机事件 D、“ 是有理数, ”是不可能事件8. 已知,如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的有( )( 1 )AD平分∠EDF;(2)△EBD≌△FCD;(3)BD=CD;(4)AD⊥BC.
 A、1个 B、2个 C、3个 D、4个9. 如图(1)是长方形纸片, ,将纸片沿AC折叠成图(2),再沿EC折叠成图(3),则图(3)中 为( )
A、1个 B、2个 C、3个 D、4个9. 如图(1)是长方形纸片, ,将纸片沿AC折叠成图(2),再沿EC折叠成图(3),则图(3)中 为( ) A、 B、 C、 D、10. 小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,小明从家到学校行驶路程s(m)与时间t(min)的大致图象是( )A、
A、 B、 C、 D、10. 小明从家到学校,先匀速步行到车站,等了几分钟后坐上了公交车,公交车沿着公路匀速行驶一段时间后到达学校,小明从家到学校行驶路程s(m)与时间t(min)的大致图象是( )A、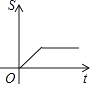 B、
B、 C、
C、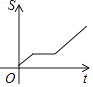 D、
D、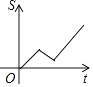
二、填空题
-
11. 2018年11月 19日,我国成功发射了第四十二、第四+三颗北斗导航卫星,中国北斗卫星导航系统是中国自行研制的全球卫星导航系统,可为用户提供定位、导航、授时服务,定位精度10米,测速精度0.2米/秒,授时精度0.00000001秒.其中0.00000001用科学记数法表示为.12. 一个含30°角和另一个含45°角的三角板按如图所示放置,直角顶点重合,且两条斜边 ,则 °.
 13. 一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格形状大小完全相同,当蚂蚁停下时,停在地板中阴影部分的概率为 .
13. 一只蚂蚁在如图所示的方格地板上随机爬行,每个小方格形状大小完全相同,当蚂蚁停下时,停在地板中阴影部分的概率为 . 14. 如图,B,D,E,C在一条直线上,且 ,若 ,则 .
14. 如图,B,D,E,C在一条直线上,且 ,若 ,则 . 15. 已知:如图,在长方形 中, 延长 到点 ,使 ,连接 ,动点 从点 出发,以每秒2个单位长度的速度沿 向终点 运动,设点 的运动时间为 秒,当 的值为时, 和 全等.
15. 已知:如图,在长方形 中, 延长 到点 ,使 ,连接 ,动点 从点 出发,以每秒2个单位长度的速度沿 向终点 运动,设点 的运动时间为 秒,当 的值为时, 和 全等.
三、解答题
-
16. 先化简,再求值: ,其中 , .17. 如图,直线AB//CD,BC平分∠ABD,∠1=54°,求∠2的度数.
 18. 如图, 相交于点 , .那么 与 相等吗?请说明理由.
18. 如图, 相交于点 , .那么 与 相等吗?请说明理由. 19. 如图,在正方形网格中,每个小正方形的边长都为1,网格中有两个格点A、B和直线 .
19. 如图,在正方形网格中,每个小正方形的边长都为1,网格中有两个格点A、B和直线 .
①求作点A关于直线 的对称点 ;
② 为直线 上的点,连接 、 ,求 周长的最小值.
20. 如图,在 中: (1)、作 的平分线交AC于D,作线段BD的垂直平分线EF分别交AB于E,BC于F,垂足为点 .(尺规作图,保留作图痕迹,不写作法)(2)、在(1)的条件下,连接DF,判断DF与边AB的位置关系为(直接写出结果,不用说明理由)21. 现有足够多除颜色外均相同的球,请你从中选12个球设计摸球游戏.(1)、使摸到红球的概率和摸到白球的概率相等;(2)、使摸到红球、白球、黑球的概率都相等;(3)、使摸到红球的概率和摸到白球的概率相等,且都小于摸到黑球的概率.22. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离 (米)与甲出发的时间 (分)之间的关系如图所示,
(1)、作 的平分线交AC于D,作线段BD的垂直平分线EF分别交AB于E,BC于F,垂足为点 .(尺规作图,保留作图痕迹,不写作法)(2)、在(1)的条件下,连接DF,判断DF与边AB的位置关系为(直接写出结果,不用说明理由)21. 现有足够多除颜色外均相同的球,请你从中选12个球设计摸球游戏.(1)、使摸到红球的概率和摸到白球的概率相等;(2)、使摸到红球、白球、黑球的概率都相等;(3)、使摸到红球的概率和摸到白球的概率相等,且都小于摸到黑球的概率.22. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离 (米)与甲出发的时间 (分)之间的关系如图所示, (1)、甲步行的速度为米/分;(2)、乙走完全程用了分钟;(3)、求乙到达终点时,甲离终点的距离是多少米?23. 已知点C是AB上的一个动点.
(1)、甲步行的速度为米/分;(2)、乙走完全程用了分钟;(3)、求乙到达终点时,甲离终点的距离是多少米?23. 已知点C是AB上的一个动点. (1)、问题发现
(1)、问题发现如图1,当点C在线段AB上运动时,过点C作 ,垂足为点C,过点A作 ,垂足为点A,且 , .
① 与 全等吗?请说明理由;
②连接DE,试猜想 的形状,并说明理由;
③ 是否成立?_▲_(填“成立”或“不成立”).
(2)、类比探究如图2,当点C在线段AB的延长线上时,过点C作 ,垂足为点C,过点 作 ,垂足点A,且 , .试直接写出 的形状为;此时线段DC、AE和AC之间的数量关系为(直接写出结论,不用说明理由).