初中数学苏科版九年级上册1.3 一元二次方程根与系数的关系 同步练习
试卷更新日期：2020-07-29 类型：同步测试
一、单选题
-
1. 已知x1 ， x2是一元二次方程 的两根，则x1＋x2的值是（ ）A、0 B、2 C、－2 D、42. 若 、 是方程 的两个根，则 的值为（ ）A、 B、-1 C、3 D、-33. 已知 、 是一元二次方程 的两个根，则 等于（ ）A、4 B、 1 C、
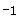D、
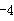4. 已知关于x的一元二次方程x2+5x﹣m＝0的一个根是2，则另一个根是（ ）A、﹣7 B、7 C、3 D、﹣35. 已知x1 ， x2是方程x2﹣3x﹣2＝0的两根，则x12+x22的值为（ ）A、5 B、10 C、11 D、136. 设 ， 是方程 的两个根，则 的值为（ ）A、 B、 C、 D、7. 设m、n是一元二次方程x2+2x﹣7=0的两个根，则m2+3m+n=（ ）A、﹣5 B、9 C、5 D、78. 若α，β为方程2x2－5x－1＝0的两个实数根，则2α2＋3αβ＋5β的值为（ ）A、－13 B、12 C、14 D、159. 已知一元二次方程a(x-x1)(x-x2)=0(a≠0，x1≠x2)与一元一次方程dx+e=0有一个公共解x=x1 ， 若一元二次方程a(x-x1)(x-x2)+(dx+e)=0有两个相等的实数根，则（ ）A、a(x1-x2)=d B、a(x2-x1)=d C、a(x1-x2)²=d D、a(x2-x1)2=d二、填空题
-
10. 设x1 ， x2是一元二次方程x2+5x﹣3=0的两根，且2x1（x22+6x2﹣3）+a=4，则a= ．
11. 已知关于 的方程 两个根是互为相反数，则 的值为.12. 已知m、n是关于x的一元二次方程x2+px+q＝0的两个不相等的实数根，且m2+mn+n2＝3，则q的取值范围是 ．13. 若方程 的根也是方程 的根，则 .14. 关于x的一元二次方程 的两个实数根分别是x1、x2 ， 且 ，则 的值是 ．
三、综合题
-
15. 已知关于x的方程x2＋(2k+1)x＋k2＋1＝0有两个实数根x1 ， x2.(1)、求实数k的取值范围；(2)、若x1 ， x2.满足｜x1｜＋｜x2｜＝x1x2求实数k的值．16. 我们在探究一元二次方程根与系数的关系中发现：如果关于x的方程x2+px+q＝0的两个根是x1 ， x2 ， 那么由求根公式可推出x1+x2＝﹣p ， x1•x2＝q ， 请根据这一结论，解决下列问题：(1)、若α，p是方程 的两根，则α+β＝ ， α•β＝；若2，3是方程 的两根，则m＝ ， n＝；(2)、已知a ， b满足 ，求 的值；(3)、已知a ， b ， c满足 ，求正整数 的最小值，17. 已知方程
+px+q＝0的两个根是 
， 
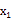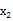，那么 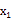+ 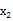＝－p， ＝q，反过来，如果 + ＝－p， ＝q，那么以 ， 为两根的一元二次方程是 +px+q＝0．请根据以上结论，解决下列问题： (1)、已知关于x的方程 +mx+n＝0(n≠0)，求出—个一元二次方程，使它的两根分别是已知方程两根的倒数．(2)、已知a、b满足 －15a－5＝0， －15b－5＝0，求 的值．
(3)、已知a、b、c均为实数，且a+b+c＝0，abc＝16，求正数c的最小值