初中数学苏科版九年级上册1.1—1.2 一元二次方程同步测试

试卷更新日期：2020-07-29 类型：同步测试

进入出卷网下载

1. 下列方程中，关于x的一元二次方程是（）

A、x²﹣x（x+3）＝0 B、ax²+bx+c＝0 C、x²﹣2x﹣3＝0 D、x²﹣2y﹣1＝0

查看试题解析
2. 一元二次方程x² ＋2x＝0的解是（）

A、x＝0 B、x＝－2 C、x₁＝2 x₂＝0 D、x₁＝－2 x₂＝0

查看试题解析
3. 用配方法解方程x²﹣6x﹣4＝0，下列配方正确的是（）

A、（x﹣3）²＝13 B、（x+3）²＝13 C、（x﹣6）²＝4 D、（x﹣3）²＝5

查看试题解析
4. 关于x的一元二次方程x²+ax-1=0的根的情况是（）

A、有两个不相等的实数根。 B、有两个相等的实数根。 C、只有一个实数根 D、没有实数根

查看试题解析
5. 已知关于x的一元二次方程 $x^{2} + b x - 1 = 0$ ，则下列关于该方程根的判断，正确的是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、实数根的个数与实数b的取值有关

查看试题解析

6. 方程 $(m + 2) x^{2}^{| m |} + 3 m x + 1 = 0$ 是关于x的一元二次方程，则m= ．

查看试题解析
7. 若x＝2是关于x的一元二次方程ax²+bx﹣8＝0（a≠0）的解，则代数式2020+2a+b的值是.

查看试题解析
8. 已知x=1是关于x的一元二次方程(1-k)x²+k²x-1=0的根，则常数k的值为。

查看试题解析
9. 如果关于 $x$ 的方程 $x^{2} - 2 \sqrt{3} x + k = 0$ 有两个相等的实数根，那么 $k$ 的值是．

查看试题解析
10. 关于x的一元二次方程（2﹣a）x²﹣2x+1＝0有两个不相等的实数根，则整数a的最小值是.

查看试题解析
11. 对于实数a，b，定义运算“◎”如下：a◎b=（a+b）²﹣（a﹣b）² ．若（m+2）◎（m﹣3）=24，则m= ．

查看试题解析
12. 已知关于x的方程a（x+m）²+b＝0（a、b、m为常数，a≠0）的解是x₁＝2，x₂＝﹣1，那么方程a（x+m+2）²+b＝0的解．

查看试题解析
13. 如图，四边形ABCD中，CD=AD，∠CDA=∠ABD=90°，点E为CD边的中点，连接BE，AB=2，BC= ，则BD=。

查看试题解析
14. 如图是一个运算程序的示意图，若输出y的值为2，则输入x的值可能为．

查看试题解析
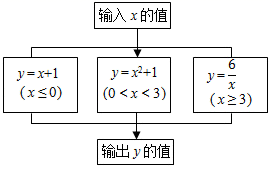15. 如图，在Rt△ABC中，∠ACB＝90°，∠A＝60°，AC＝2 $\sqrt{3}$ ，点P为AB边上的一个动点，连接PC，过点P作PQ⊥PC交BC边于点Q，则BQ的最大值为．

查看试题解析

16. 解方程：

(1)、x²﹣1＝3（x﹣1）

(2)、x²﹣4x＝－1

查看试题解析
17. 解下列方程：

(1)、x²﹣4x﹣5＝0；

(2)、（x+1）²＝2（x+1）.

查看试题解析
18. 已知关于x的方程 $m x^{2} - (2 m + 1) x + 2 = 0 (m \neq 0)$ ．

(1)、求证：方程总有两个实数根；

(2)、若方程的两个根均为正整数，写出一个满足条件的m的值，并求此时方程的根．

查看试题解析
19. 已知关于 $x$ 的方程 $x^{2} + (k + 1) x + k - 2 = 0$ .

(1)、求证：不论 $k$ 取何实数，此方程都有两个不相等的实数根；

(2)、若此方程的一个根为 $- 3$ ，求 $k$ 的值.

查看试题解析
20. 已知关于x的一元二次方程(a+b)x²+2cx+(b-a)=0，其中a、b、c分别为 $△ A B C$ 三边的长.

(1)、如果 $x = - 1$ 是方程的根，试判断 $△ A B C$ 的形状，并说明理由.

(2)、如果方程有两个相等的实数根，试判断 $△ A B C$ 的形状，并说明理由.

(3)、如果 $△ A B C$ 是等边三角形，试求这个一元二次方程的根.

查看试题解析

初中数学苏科版九年级上册1.1—1.2 一元二次方程 同步测试