人教新课标A版 必修一 1.3.2奇偶性
试卷更新日期:2020-07-29 类型:同步测试
一、单选题
-
1. 下列函数为偶函数的是( )A、 B、 C、 D、2. 已知f(x)是R上的偶函数,当x≤0时,f(x)=x+1,则f(x2)的表达式为( ).A、-(x+1)2+1 B、(x+1)2 C、x2-1 D、-x2+13. 下列函数是奇函数的是( )A、 B、 C、 D、4. 已知函数 是奇函数,且 ,则 ( )A、 B、 C、 D、5. 函数 的图象大致为( )A、
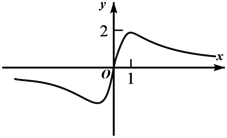 B、
B、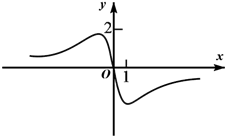 C、
C、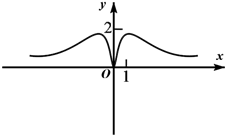 D、
D、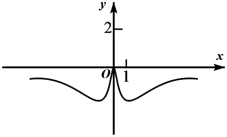 6. 已知 是定义在R上的偶函数,并满足 ,当 时, ,则 ( )A、4.5 B、-4.5 C、0.5 D、-0.57. 已知函数 ,则( )A、 B、 的定义域为 C、 为偶函数 D、 在 上为增函数8. 函数 在 单调递减,且为奇函数.若 ,则满足 的x取值范围是( )A、 B、 C、 D、9. 若定义在R的奇函数f(x)在 单调递减,且f(2)=0,则满足 的x的取值范围是( )A、 B、 C、 D、10. 奇函数 在 上单调递减,且 ,则不等式 的解集是( ).A、 B、 C、 D、11. 已知定义在 上的函数 在 上是减函数,若 是奇函数,且 , 则不等式 的解集是( )A、 B、 C、 D、12. 已知定义在 上的函数 满足 ,且在 上是增函数,不等式 对于 恒成立,则 的取值范围是( )A、 B、 C、 D、
6. 已知 是定义在R上的偶函数,并满足 ,当 时, ,则 ( )A、4.5 B、-4.5 C、0.5 D、-0.57. 已知函数 ,则( )A、 B、 的定义域为 C、 为偶函数 D、 在 上为增函数8. 函数 在 单调递减,且为奇函数.若 ,则满足 的x取值范围是( )A、 B、 C、 D、9. 若定义在R的奇函数f(x)在 单调递减,且f(2)=0,则满足 的x的取值范围是( )A、 B、 C、 D、10. 奇函数 在 上单调递减,且 ,则不等式 的解集是( ).A、 B、 C、 D、11. 已知定义在 上的函数 在 上是减函数,若 是奇函数,且 , 则不等式 的解集是( )A、 B、 C、 D、12. 已知定义在 上的函数 满足 ,且在 上是增函数,不等式 对于 恒成立,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 已知一个奇函数的定义域为[a+1,b-2], 则 =.14. 若函数 为偶函数,则15. 设函数 是定义在 上的偶函数,记 ,且函数 在区间 上是增函数,则不等式 的解集为16. 已知函数 满足 ,对任意的 都有 恒成立,且 ,则关于 的不等式 的解集为 .
三、解答题
-
17. 判断下列函数的奇偶性(1)、(2)、18. 已知函数 在定义域 上是奇函数,又是减函数,若 ,求实数 的范围.19. 已知函数 的图像经过点(1)、求 的值并判断 的奇偶性;(2)、判断并证明函数 在 的单调性,并求出最大值.
